Entropic Uncertainty Relations and Mutual Information Correlation Sums in Two-level Superposition States of Coupled Oscillators

Abstract

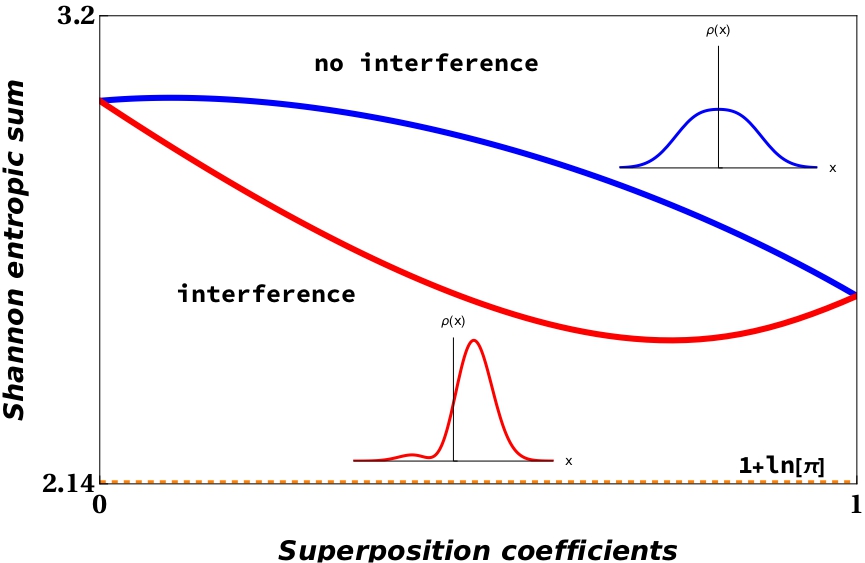
The effects of quantum interferences and interaction strength on the entropic uncertainty relations, and on mutual information correlation sums, are examined in two-level superposition states of two coupled oscillators. The presence of quantum interferences results in a movement of the entropy sums toward the uncertainty relation bound, for both attractive and repulsive interaction potentials. On the other hand, these interferences suppress the statistical correlations in the presence of an attractive potential, while the correlations increase for a repulsive one. In general, stronger interactions between particles move the entropy sums away from bound, with the result that the systems possess larger statistical correlations. However, there are superposition and attractive interaction regimes, where the entropy sum of an interacting system can actually lie closer to the bound, in comparison to the corresponding non-interacting one. In these cases, the statistical correlations between particles is lesser for the interacting systems, as compared to the non-interacting ones. These effects are not observed when repulsive potentials are present. Here, the non-interacting systems lower-bound both the entropy sums and correlation measures. These results offer insights into the nature of superposition or quantum interference effects in interacting quantum systems, and the behavior in terms of the entropic uncertainty relations, statistical correlations and interaction strength.

Resumen. Se examinan los efectos que las interferencias cuánticas y la magnitud de la interacción tienen sobre las relaciones de incertidumbre entrópicas, así como sobre las sumas correlaciones me didas a través de la información mutua, en estados de superposición de dos niveles de dos osciladores acoplados. La presencia de interferencias cuánticas da como resultado un movimiento de las sumas entrópicas hacia la cota de la relación de incertidumbre, tanto para potenciales de interacción atractivos como repulsivos. Por otra parte, en presencia de un potencial atractivo, estas interferencias suprimen las correlaciones estadísticas, mientras que las correlaciones aumentan en presencia de uno repulsivo. En general, con interacciones más fuertes entre partículas, las sumas de entrópicas se alejan de la cota, dando como resultado mayores correlaciones estadísticas en los sistemas. Sin embargo, existen regímenes de superposición e interacción atractiva, en los cuales la suma entrópica de un sistema interactuante puede estar más cerca de la cota, en comparación con el sistema no interactuante correspondiente. En estos casos, las correlaciones estadísticas entre partículas son menores para los sistemas interactúantes que para los no interactuantes. Estos efectos no se observan en los potenciales repulsivos. En este caso, los sistemas no interactuantes establecen límites inferiores tanto para las sumas entrópicas como para las medidas de correlación. Estos resultados dan información sobre la naturaleza de los efectos de superposición o interferencia cuántica en sistemas cuánticos interactuantes, y su comportamiento en términos de relaciones de incertidumbre entrópica, correlaciones estadísticas y fuerza de interacción.