Journal of the Mexican Chemical Society, vol. 65, no. 3, 2021
Sociedad Química de México A.C.
Ali Zolfagharia
University of Kashan, Iran
Mehran Riazian *
Islamic Azad University, Iran
Mohsen Ashjari
University of Kashan, Iran
Received: 11 February 2021
Accepted: 14 April 2021
Abstract: This research firstly aims to fabricate and characterize doped TiO2 nanoparticles (NPs) by iron and Sulphur dopants, and then the determination of the photocatalytic activity of NPs. Titanium tetraisopropoxide (TTIP), iron trichloride hexahydrate, thiouria, glacial acetic are utilized as precursors in the hydrothermal method without using a template or surfactant. The synthesized NPs are investigated by X-ray diffraction (XRD), field emission electron microscopy (FE-SEM), energy-dispersive X-ray spectroscopy (EDX), transmission electron microscopy (TEM), N2 adsorption-desorption, UV-Vis spectroscopy, UV-Vis diffuse reflectance spectroscopy (DRS) and Fourier transform infrared (FT-IR). The lattice constants, strain, stress, deformation energy density and crystallite size are investigated using Williamson -Hall (W-H) and Wagner-Halder (W-H) models by considering the different isotropic nature of the crystalline lattice. The X-ray analysis indicates the tetragonal anatase phase without dopant crystalline phases. The FE-SEM and TEM images reveal a granular shape of NPs with a mean diameter of about 35 nm. Decoloration or photodegradation of organic dyes such as methylene blue (MB) and Evans Blue (EV) under UV -Vis irradiation is a method to measure the photocatalytic activity of doped TiO2 NPs. The results indicate the significant effect of dopants on the photocatalytic activity of doped TiO2 NPs, so that in comparison with other studies, it has a higher performance and removal efficiency. The bandgap of NPs is estimated from the Kubelka-Munk theory to be 2.87 eV.
Keywords: Photocatalytic, TiO2, iron and sulphur, hydrothermal method, dopants.
Resumen: Esta investigación tiene como objetivo fabricar y caracterizar nanopartículas de TiO2 (NP) dopadas con hierro y azufre, y la actividad fotocatalítica de las NP. El tetraisopropóxido de titanio (TTIP), el tricloruro de hierro hexahidratado, la tiouria, el acético glacial fueron los precursores en la síntesi según el método hidrotermal y no se utilizó una plantilla o tensioactivo. Las NP sintetizadas se caracterizaron por difracción de rayos X (XRD), microscopía electrónica de emisión de campo (FE-SEM), espectroscopía de rayos X de dispersión de energía (EDX), microscopía electrónica de transmisión (TEM), adsorción-desorción de N2, espectroscopías UV-Vis, de reflectancia difusa UV-Vis (DRS) e infrarroja por transformada de Fourier (FT-IR). Las constantes de red, deformación, tensión, densidad de energía de deformación y tamaño de cristal se investigan utilizando modelos de Williamson-Hall (W- H) y Wagner- Halder (W-H), considerando la diferente naturaleza isotrópica de la red cristalina. El análisis de difracción de rayos X indica la fase anatasa tetragonal sin fases cristalinas dopantes. Las imágenes FE-SEM y TEM revelan una forma granular de las NP, con un diámetro promedio de aproximadamente 35 nm. La decoloración o fotodegradación de tintes orgánicos como el azul de metileno (MB) y el azul de Evans (EV) bajo irradiación UV-Vis es un método para medir la actividad fotocatalítica de las NP de TiO2 dopadas. Los resultados indican un efecto significativo de los dopantes sobre la actividad fotocatalítica de las NP de TiO2 dopadas, que, en comparación con otros estudios, tiene un mayor rendimiento y eficiencia de eliminación. La bandgap de las NP se estimó en 2.87 eV, a partir de la teoría de Kubelka-Munk.
Palabras clave: Fotocatalítico, TiO2, hierro y azufre, método hidrotermal, dopantes.
Introduction
In recent decades, the transition-metal oxide semiconductor, especially TiO2 Nps has been extensively subjected due to outstanding and versatile applications in photodegradation of dyes, solar cells, photo-chemical sensors, anti-fog glasses, self-cleaning covers, fuel cells, etc [1-6]. In addition, due to excellent properties such as low cost, none-toxicity, large bandgap about 3.2 eV, high oxidizing ability, high resistance against corrosion, it plays an important role in photovoltaic, electrochromic devices and degradation of complex-organic pollutants and infrangible Azo-dyes. TiO2 reveals three common crystalline phases including anatase, rutile, and brookite, whilst the photocatalytic activity is practicable in anatase crystalline phase. Many researchers investigated and characterized the heterogeneous and doped TiO2 Nps due to the large bandgap of anatase [7-10]. Dopants and composites could modify and make active Nps upon the maximum absorption wavelength λ_max≤387 nm in UV irradiation for the pure anatase phase. The λ_max is a limitation to employ the various applications in visible light range [11,12]. Therefore, photocatalytic sensitivity and high oxidizing power have been improved by shifting the optical absorption edge from UV to visible region [13-15]. For this purpose, ceramic and metal ions as dopants are embedded into the TiO2 matrix. Of course, doping the metal atoms produce electron traps in the metal centers, while at the same time, the thermal stability (phase transformation) of the final product decreases. To transcend the obstacle and also increase the bandgap range, simultaneous ceramic-metal doping has been investigated and many ceramic-metal components have been widely researched [16-24].
Influential structural factors such as particle size, morphology, lattice parameters, synthesis method, particle dimensions, and adsorption-desorption of particle surface could drastically affect the performance and efficiency of the fabricated nano -photocatalysts [25-27]. The lattice structure of NPs effectively depends on crystallite size, crystalline phase stability the lattice imperfection. The finite crystallite size and dimension causes imperfection and lattice defects. The lattice imperfection involves lattice dislocations, stress, stacking faults, ad-atoms and grain boundary triple junction that could lead to broadening the peaks of XRD spectra. The lattice structural parameters including size, stress, strain, strain energy density of NPs are calculated by the W-H and H-W models.
Various fabrication methods have been performed to synthesis TiO2 NPs such as sol-gel [28,29], microemuolsion, reverse micells [30-33], Co-precipitation [34,35], pyrolysis [36,37], laser ablation [38,39], chemical vapor deposition [40,41], physical vapor deposition [42,43], solvo-thermal [44,45], electrochemical deposition [46,47], mechano-chemical [48,49], combustion [50,51], sono- chemical microwave [52,53] and hydrothermal [54,55]. Among of them, the hydrothermal method possesses more benefits such as cheap cost, controllable in synthesis, productive, no needing thermal operation and low pollutions [56-58].
Nowadays, with the advancement of technology and industrial products, the elimination of wastewater and residue materials from the production cycle are vital and important. Most of the waste compounds are complex, toxic, mutagenic, carcinogenic and do not degrade easily in the soil or water, consequently, pollute the environment.
Conventional oxidation methods cannot diminish the complex organic contaminant, particularly the textile dyes. The advanced oxidation processes have been intensely degraded the detrimental and indecomposable(.OH−andcomplex.H+) pollutants to simple and environmentally friendly compounds via highly reactive radicals . In this research, Fe-S co -doped titanium oxide has been specified and fabricated by the hydrothermal method. Also, the photocatalytic activity of the doped TiO2 NPs has been measured under UV-Vis exposure by decoloring the common and overused textile dyes methylene blue and Evans blue.
Compared to the existing research, the present study has performed the prominent results in specific surface area and photodegradation efficiency [6,59,60].
Experimental
Procedures and Details
The Fe-S doped TiO2 NPs are prepared from titanium tetraisopropoxide (TTIP) (Merck, 98%), iron (III) nitrate nonahydrate (Fe(NO3)3.9(H2O) (Merck, 98%), thiourea (Merck, 97%), glacial acetic acid (Merck, 99%), methylene blue (Merch, 98%), Evans blue (Merck, 98%) and deionized water as precursors without any further impurity. The molar ratio of the applied precursors is TTIP/acetic acid/thiouria/iron (III) nitrate nonahydrate/deionized water = 1: 9.95: 0.01: 0.02: 247. Firstly, 38.5 mL of glacial acetic acid poured into the ice bath container, then 20 mL of TTIP is dropwisely added, while the suspension is vigorously stirred by a magnetic stirrer for 30 minutes. A certain amount of deionized water, thiourea and iron (III) nitrate nonahydrate according to the mentioned molar ratio are dropwisely blended in a separate container and stirred for 2 hours. Afterward, the mixed suspension is added to the starting suspension in the ice bath container, stirred for 5 hours and ultimately, sonicated for 15 minutes at 45 kHz (Model: Sono Swiss). The resulting suspension is placed in stainless- steel autoclave including a Teflon wall-mounted container with an inner volume of 100 mL. The chemical reaction is accomplished at 180±1 oC and 10±0.1 bar for 24 hours. Subsequently, the obtained suspension is dried in the oven for 24 hours at 70 oC and purified several times thoroughly with deionized water to eliminate any residual ions. At last, the soft and dry bulk is grounded by agar mortar and converted to a soft and smooth powder.
XRD pattern is recorded using (model: GBC-MMA) with CuKα radiation (λ= 0.15418 nm) equipped with a Nickel filter. The XRD patterns of doped TiO2 nano-crystallites are recorded in a range of 10o ≤ 2θ ≤ 80o with a step rate of 2 degrees/min and 0.02o step size at room temperature.
The morphology of the NPs is investigated by TEM (model: Philips CM120) and FE-SEM (model: Hitachi S-4160) equipped with the EDX. The photocatalytic activity of the NPs is determined by the photodegradation of MB and EB aqua suspension under UV (Lamp: Philips, UV-A 253.70 nm, 40 W) and Visible light (Lamp: LED, 40 W) radiation using the UV -Vis spectrophotometer (model: Varian 50 scan). The chemical binding of doped NPs is specified by the FT-IR (model: Perkin-Elmer Pyris) spectrum recorded in the range of 400 -4000 cm-1 using KBr pellets. The optical absorption of NPs is calculated in the range of 190- 800 nm by using a UV-Vis spectrophotometer (model: Shimadzu UV-2550-8030) with a slit width of 0.5 nm and light source wavelength of 360 nm at room temperature.
Results and discussion
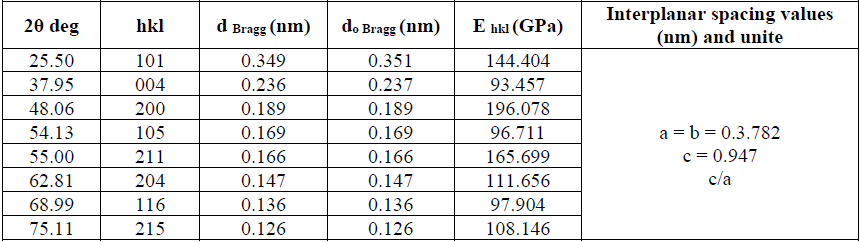
The diffraction pattern reveals sharp peaks confirmed to a single crystalline phase of the tetragonal anatase structure without the presence of iron and sulfur dopant crystalline phases. Fig. 1 indicates the prominent XRD peaks, where are located at the specific 2θ and belongs to the Miller indices (hkl): (101), (004), (200), (105), (211), (204), (116), (215), corresponding to the TiO2 anatase (space group I41/amd), Crystallography Open Database (COD) card no. (96-153-0152), a=b= 0.378 nm and C= 0.951 nm.
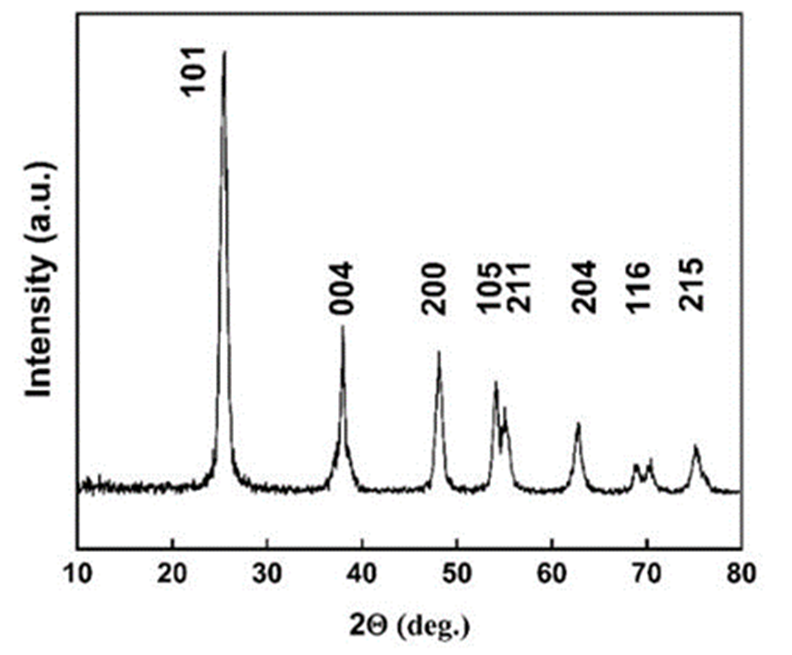
Fig. 1
XRD patterns of anatase crystalline phase of doped TiO2 NPs.
The imperfection of crystallinity causes a broadening of the diffraction peak. The peak broadening is assigned to the crystallite size induced and lattice strain. Instrumental and sample-dependent consideration determine the total breadth of the XRD peaks. To accurate analysis, it is clear to refine a measured broadening of the diffraction pattern (βm) from the instrumental broadening including diffraction patterns of standard material such as silicon (βins). This correction assigns as follow:
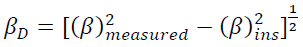 (1)
(1)where 𝛽𝐷 is the corrected broadening. The crystallite size of TiO2 NPs is determined by the Scherrer's equation from the prominent peaks:
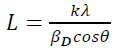 (2)
(2)where L is the crystallite size in nm, k is a shape factor equal to 0.9 for spherical shaped particles, λ is the x-ray radiation wavelength (0.15418 nm), βD is the corrected peak width at the half-maximum intensity in radians and θ is the prominent peak position in half diffraction angle (Bragg's angle). The Scherrer equation is a simple and incomplete estimate that considers crystallites to be a spherical shape. According to the Scherrer's equation, the crystallite size is calculated from the most intense XRD peak (101) to be 11 nm. The presence of the iron and sulfur dopants resulted in the XRD peak shifts, crystallite size and lattice strain, which is associated with the lattice stress generated. The lattice parameters, interplanar space values (d-space) and unit cell volume of the anatase crystalline phase (V) could be measured using the Bragg's equation (nλ=2d sinθ) and the lattice geometry equation as given:
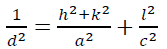 (3)
(3)
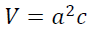 (4)
(4)The XRD data and lattice parameters are tabulated in Table 1. The x-ray density (Dx) and the specific surface area (Sa) of the doped TiO2 nanocrystallites along the prominent Bragg peak (101) are estimated by the following equations [61]:
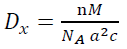 (5)
(5)
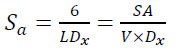 (6)
(6)
Structure data of anatase crystalline phase of the pure and doped TiO2 NPs.
where M is the molecular weight, n is the number of atoms associated with each unit tetragonal cell, a and c are lattice constants, L is the doped TiO2 nanocrystallite size, V is the volume of the spherical nanocrystallites 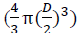 , NA denotes the Avogadro's constant and L is the doped TiO2 nanocrystallite size. The Sa and Dx are calculated to be 92.97
, NA denotes the Avogadro's constant and L is the doped TiO2 nanocrystallite size. The Sa and Dx are calculated to be 92.97 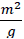 and 3.92
and 3.92 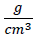 , respectively.
, respectively.
Dislocation affects the crystallite size and lattice strain (ɛ) by broadening the diffraction peaks [62]. The dislocation density (δ) is defined as the number of defects in the crystalline lattice that could be estimated by the experimental relationship with crystallite size from the below formula:
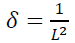 (7)
(7)According to the W-H method, peak broadening is due to the contribution of the crystallite size induced and lattice strain-induced. Therefore, the total peak width is assumed to be independent and could be ascribed by the W-H equation:
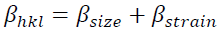 (8)
(8)
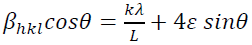 (9)
(9)Where 𝛽khl,λ and 𝜀𝜀 are the total integral breadth of Bragg peak, the x-ray wavelength and the lattice strain, respectively. Relation (9) introduces the uniform deformation model (UDM), where lattice strain and deformation are assumed to be uniform in all crystallographic directions. This model assumes that the isotropic nature of the crystallite and the material properties are independent of the measured directions. According to UDM, the value of 𝛽hklcosθ versus 4 sinθ is plotted, moreover, the lattice strain and the crystallite size are determined from the slope and intercept of the linear fit, respectively (Fig. 2(a)).

Fig. 2
The modified models of W-H and H-W analysis of anatase crystalline phase of TiO2 NPs.
In the uniform deformation strain model (USDM), the nature of the crystallite and the lattice strain is assumed to be anisotropic, as well as the relation between 𝜀𝜀 and stress (𝜎𝜎) to be linear according to the Hook's law:
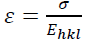 (10)
(10)where, Ehkl is the modulus of elasticity (Young's modulus) in the direction perpendicular to the (hkl) plane. Ehkl and the dependence with their elastic compliances Sij for the tetragonal crystalline phase are presented by the following equation:
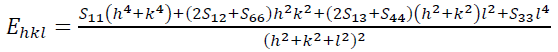 (11)
(11)where S11, S12, S13, S33, S44 and S66 are the elastic compliances of anatase TiO2 crystalline phase and their values are: 5.1×10−12,−0.8×10−12 ,−3.3×10−12, 10.7×10−12 , 18.5×10−12 and 16.7×10−12 𝑚𝑚2𝑁𝑁−1, respectively [63]. In this model, the lattice strain in the W-H equation is substituted by the recent approximation value of the 𝜀 in the second term of equation (9) results:
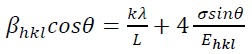 (12)
(12)The uniform stress 𝜎 and the crystallite size could be calculated from the slope and the
y-intercept of the linear fit of line plotted between 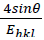 and βhkl , respectively
(Fig. 2(b)).The average
Young's modulus (Ehkl,) for the
tetragonal anatase crystalline phase is calculated as 123.003 GPa. The uniform 𝜀𝜀
could be measured by:
and βhkl , respectively
(Fig. 2(b)).The average
Young's modulus (Ehkl,) for the
tetragonal anatase crystalline phase is calculated as 123.003 GPa. The uniform 𝜀𝜀
could be measured by:
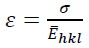 (13)
(13)The uniform deformation energy density model (UDEDM) could be utilized to specify the deformation energy density (u), crystallite size, lattice strain, and stress. In many cases, the mentioned models are not complete due to considering the homogenous isotropic nature of crystalline aspects. By including the micro-strain and isotropic diffraction domains, the proportionality in strain-stress correlation are dependent. The value of (u) can be determined from the Hook's law and the dependence between u and lattice strain is given by:
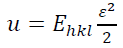 (14)
(14)
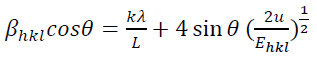 (15)
(15)
Fig. 2(c) reveals the plot of 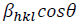 versus
versus 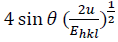 . The value of u and the crystallite size are estimated from the slope and y-intercept of linear fit, respectively. The 𝜎 and 𝜀 could be determined by
. The value of u and the crystallite size are estimated from the slope and y-intercept of linear fit, respectively. The 𝜎 and 𝜀 could be determined by 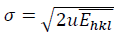 and
and 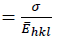 , respectively.
, respectively.
The W-H method essentially assumes that the isotropic line broadening and strain effects resulted from a symmetric shift of the atoms from their ideal places and lead to point defects, dislocations and vacancies in the crystalline structure [64].
This assumption implies the diffracting domains showing isotropic nature due to the micro-strain portion. A more accurate assessment of the size-strain parameters can be carried out by considering an average size-strain plot (SSP). The Halder-Wagner (H-W) method considers the crystallite size and strain profiles as a Lorentzian and a Gaussian function, respectively [62]. According to the SSP method, less importance (weight factor) is given to the data that comes from the high-angles than the low and mid-angles that have more accuracy [62]. Consequently, the SSP method could be expressed as:
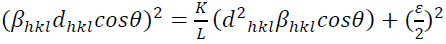 (16)
(16)where k is a shape factor, which is considered as 4/3 for spherical particles, 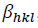 ,
, 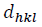 ,
, 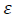 ,
, 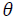 and D are the same as the quantities in the W-H equation. Fig. 2(d) reveals the variation of
and D are the same as the quantities in the W-H equation. Fig. 2(d) reveals the variation of 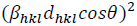 respect to
respect to 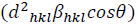 for the intensive peaks for tetragonal doped TiO2 NPs. The crystallite size and lattice strain are determined by the slope and y-intercept of the linearity fitted data, respectively. According to the XRD analysis, the nanocrystallite size increases by adding the Iron and Sulphur atoms as dopants in the anatase crystalline lattice. Also, the values of strain, stress, and deformation energy density have increased compared to the pure TiO2 NPs. This increase is attributed to the presence of iron and Sulphur atoms in the tetragonal anatase crystalline lattice and causes expansion in the primary unit cell.
for the intensive peaks for tetragonal doped TiO2 NPs. The crystallite size and lattice strain are determined by the slope and y-intercept of the linearity fitted data, respectively. According to the XRD analysis, the nanocrystallite size increases by adding the Iron and Sulphur atoms as dopants in the anatase crystalline lattice. Also, the values of strain, stress, and deformation energy density have increased compared to the pure TiO2 NPs. This increase is attributed to the presence of iron and Sulphur atoms in the tetragonal anatase crystalline lattice and causes expansion in the primary unit cell.
The various W-H and H- W models give different lattice parameters and among them, the SSP is the most appropriate method to show the most agreement with the experimental results, similarly, it indicates the least data scattering away from a linear relationship than the other W-H methods. According to Table 2, the size of nanocrystals is larger than the pure state and smaller than the doped TiO2 NPs in sol- gel synthesis. The size increase is attributed to the presence of iron and sulfur dopants in the anatase crystalline lattice. The lattice strain, stress and uniform deformation energy density is greater than the pure state and the doped TiO2 NPs in sol-gel synthesis [6]. Iron and sulfur dopants in hydrothermal synthesis cause more expansion in the crystalline lattice and increase in the lattice strain.
Geometric parameters of anatase crystalline phase of pure and doped TiO2 NPs.

Fig. 3 shows the morphology of doped TiO2 Nps. As shown, the particles are condensed with an average diameter ranging from 30 to 35 nm. The TEM image (Fig. 4(a)) confirms the morphology of the NPs and shows the formation of semi-cubic particles with an average diameter of about 30 nm. The Selected Area Electron Diffraction (SAED) pattern of doped TiO2 Nps is revealed in Fig. 4(b). The SAED pattern exhibits several numbers of rings with different intensity that is consisted of discreet diffraction spots because of the random crystalline orientations, which corresponds to the disparate diffraction planes of the TiO2 Nps [66,67]. The most intensity of the SAED pattern belongs to the (101) that indicates the tetragonal anatase phase of doped TiO2 Nps.

Fig. 3
SEM images of doped TiO2 Nps with different magnifications.

Fig. 4
(a)TEM image and (b)SAED pattern of doped TiO2 Nps.
According to EDX analysis (Fig. 5), the energy dispersive of doped TiO2 Nps confirms the presence of the Fe and S atoms in the TiO2 matrix without the unwanted and irrelevant impurity. The inset of Fig. 5 and Table 3 illustrate the distribution of atomic and weight percentage of the elements involved in the doped TiO2 NPs.
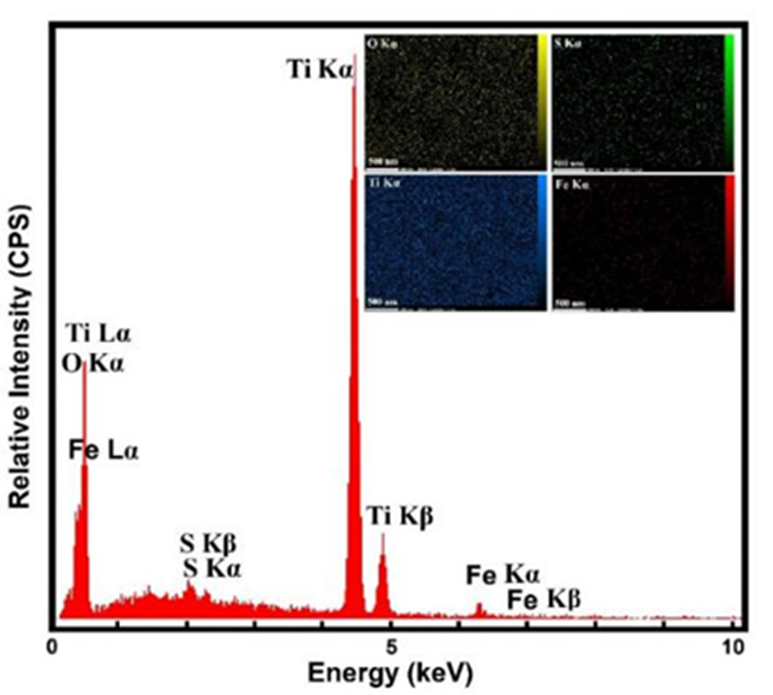
Fig. 5
EDX spectra of doped TiO2 Nps.
Elemental analysis, distribution of atomic and weight percentage of doped TiO2 Nps.

To estimate the light absorption properties and the optical absorption bandgap (Egap) of the doped TiO2 NPs, the NPs were completely homogenized and also dispersed in deionized water by the ultrasonic bath at 55 KHz for 4 minutes. The diffuse reflectance spectroscopy (DRS) spectrum of the doped NPs and the comparison with the commercial TiO2 NPs are revealed in Fig. 6. More light absorption in the UV-Vis range indicates the higher photocatalytic activity of nano-photocatalysts. The commercial TiO 2 NPs show significant absorption about 395 nm associated with the Egap of 3.2 eV due to the electron transition from the valence to the conduction band. It is noteworthy that the bandgap of the commercial TiO2 NPs could improve by doping of the modifier such as Fe and S atoms.
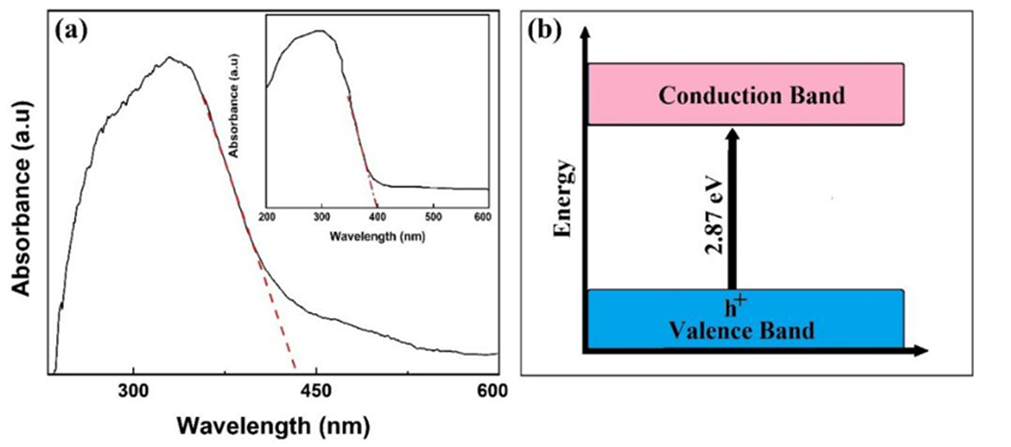
Fig. 6
(a) The optical absorption spectrum (Kubelkae-Munk function) of doped TiO2 NPs, the inset indicates the UV-Vis optical absorption of commercial TiO2 NPs, (b) Schematic diagram of energy level within the conduction and valence energy bands.
The DRS of the doped TiO2 reveals more optical absorption in the visible region than the commercial TiO 2 NPs. The E gap of the doped TiO2 NPs is calculated from the Kubelka-Munk function [68]. As shown in Fig. 6, the Egap is determined from the x-axis intercept of the linear extrapolation of the absorption edge, hence the E gap is calculated to be 2.87 eV (435 nm) and represents a red-shift compared with the commercial TiO2 NPs. The doping leads to the narrowing of the optical band and consequently the extension of the absorption region to the visible light range.
The production of the electron-hole pairs after absorbing high-energy photons, besides the delay time in their recombination process are the main challenges of the efficiency of nano-photocatalysts. By irradiating the UV-Vis light to nanoparticles, high reactive radicals, including superoxide and hydroxyl radicals are produced and attack to the complex organic pollutions and break them down to safe and simple components. The photocatalytic activity of doped TiO2 NPs is specified by measuring the photodegradation rate of dyes, including MB and EB under visible and UV irradiations.
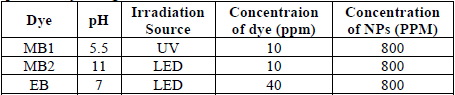
For this aim, a stock solution containing a certain amount of nano-photocatalyst in a 100 mL dye solution was provided and kept in a completely dark condition. The concentration of nano-photocatalysts and dyes, pH and radiation sources are listed in Table 4. The pH of MB1 is kept at 5.5 without any additives or controllers due to its acidic strength. The MB2 is fixed at pH=11 by sodium hydroxide solution. The EB is neutral at the pH of the solution and no additive is27utilized±1. Throughout the experiment time, the ambient temperature of the photoreactor was kept constant at 27 ± oC by a small ventilator.
Dyes and photocatalytic degradation conditions.
To measure the dye concentration, every 30 minutes 5 mL of stock solution was separated and ultrasound at 45 KHz for 6 minutes in a dark ambient so that the NPs dispersed uniformly and the absorption-desorption equilibrium was possible. The solution was then irradiated by UV-Vis light for 30 minutes at periodic intervals (30, 60, 90 and 120 minutes). The UV. irradiation source was mercury (Philips, 40 W, UV-A, 315-400 nm) and visible light lamp was LED (white, 40W), which were located at 15 cm distance from suspension container. After irradiation, the solution was passed through a 0.2 micro -pore membrane to eliminate the suspended NPs. Finally, the absorption spectra of color solutions were determined by UV-Vis spectrophotometer at 668 nm and 680 nm for MB and EB, respectively (Fig. 7).
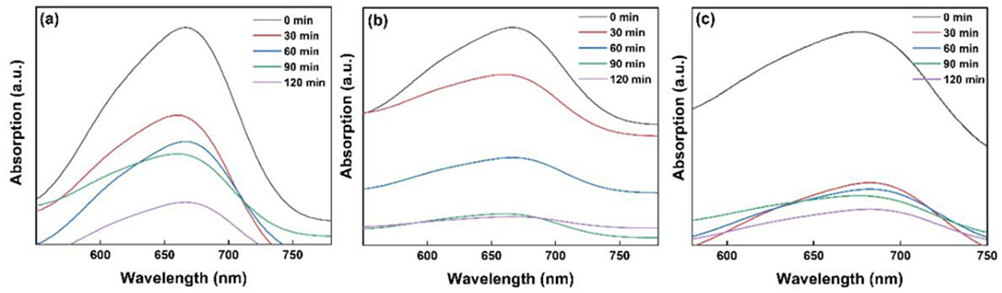
Fig 7
UV -Vis absorption spectrum of (a) MB1, (b) MB2 and (c) EB aqueous solution in the presence of doped TiO2 Nps.
The absorption intensity of dyes spectra decreases as the irradiation time increases due to photodegradation of the dyes complex [69,70]. The plots of Fig. 8(a) show the variation of 0 against the time irradiation and reveal the photodegradation percent after 120 minutes irradiation about 88%, 94% and 92% for MB1, MB2 and EV, respectively (Fig. 8(b)). The photocatalytic activity of the doped TiO2 NPs can be estimated by calculating the photodegradation rate of the dyes solution that is influenced by the doped TiO2 NPs under UV-Vis irradiation determined as comparative dependence:
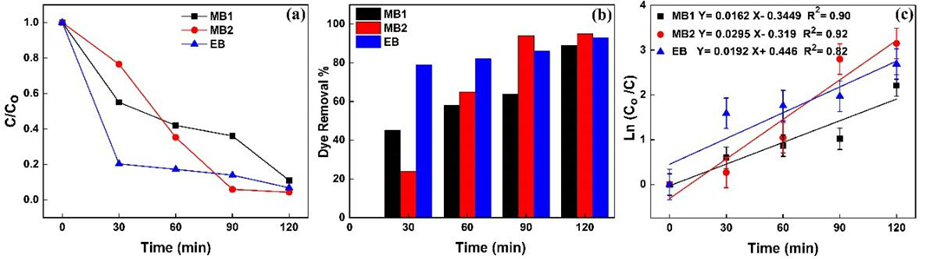
Fig. 8
(a) Photocatalytic degradation of MB1, MB2 and EB against irradiation time, (b) the dye removal percent versus irradiation time for MB1, MB2 and EB, (c) the kinetic linear relation between Ln(Co/C) and irradiation time for MB1, MB2 and (c) EB.
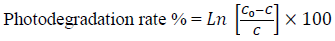 (17)
(17)where C and Co are the equilibrium and initial concentration of dyes (MB and EB), respectively. The calculation of photocatalytic activity of doped TiO2 NPs can be estimated by the pseudo-first kinetic model proposed by Langmuir-Hinshelwood equation [63]:
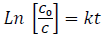 (18)
(18)where k indicates photodegradation rate constant in terms of 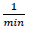 . Fig. 8(c) illustrates the variation of relative logarithmic concentration of dyes versus the irradiation time. The photocatalytic activity of doped TiO2 NPs is calculated from the degradation slope of the logarithmic dyes concentration (MB1, MB2 and EB) as 0.0162, 0.0295, 0.0192
. Fig. 8(c) illustrates the variation of relative logarithmic concentration of dyes versus the irradiation time. The photocatalytic activity of doped TiO2 NPs is calculated from the degradation slope of the logarithmic dyes concentration (MB1, MB2 and EB) as 0.0162, 0.0295, 0.0192  , respectively.
, respectively.
To investigate the chemical bonds of metallic and ceramic oxides of doped TiO2 NPs, the FTIR spectrum in the range of 400-4000 cm-1 is utilized as presented in Fig. 9. As shown in Fig. 9, characteristic peaks are at 3427, 1633, 1384, 1135 and 447 cm-1. The peak at 3427 cm-1 is attributed to the anti-symmetrical and symmetrical vibrational modes of the hydroxyl group of water and alcohol trapped in the TiO2 cavities. Furthermore, the band 1633 cm-1 is assigned to the bending vibration of hydroxyl groups. As shown, the peak at 447 cm−1 indicates Ti−O stretching vibrations, which can be related to the formation of TiO2 nanoparticles in the anatase crystalline phase [69,70]. The presence of absorption bands at 1384 cm-1 and 1135 cm- 1 are attributed to the formation of Ti-O-S bonds that occurred through a bidentate SO42- co-ordinated to Ti4+ [71].
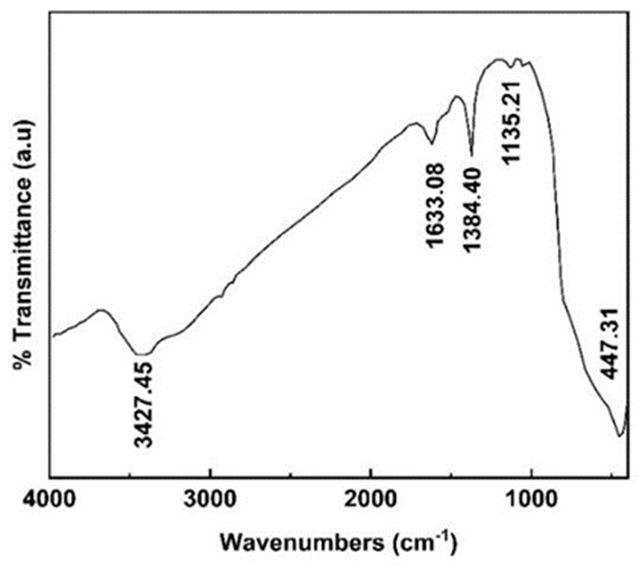
Fig. 9
FTIR spectra of doped TiO2 Nps.
The BJH (Burret-Joyner-Halenda), Brunauer-Emmet- Teller (BET),
α
s- plot, t-plot, MP-plot and Langmuir isotherms were carried out to determine the physical surface, Porosity, layer thickness, pore size distribution and porosity of doped TiO2 NPs by measuring the adsorption in terms of the relative pressure in static equilibrium. For this purpose, the nitrogen gas adsorption-desorption isotherm was measured at 77 Kelvin. By comparing the N2 physisorption isotherm by the International Union of Pure and Applied Chemistry (IUPAC) classification, Fig. 10(a) attributes the adsorption-desorption to the type IV and the hysteresis loop belongs to H2 type over the range of 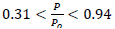 . The hysteresis loop in the isotherm indicates the presence of mesoporosity in the material and its shape can be used to obtain information about the geometry of the cavities. This adsorption-desorption isotherm denotes capillary condensation in meso and macropores, whereas closure at about
. The hysteresis loop in the isotherm indicates the presence of mesoporosity in the material and its shape can be used to obtain information about the geometry of the cavities. This adsorption-desorption isotherm denotes capillary condensation in meso and macropores, whereas closure at about 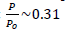 shows the presence of small mesopores. The other porosity parameters including Burret-Joyner-Halenda (BJH) pore size distribution, the BET specific surface area (SBET) and the volume of adsorbed gas to form a single layer on the surface under STP condition (Vm) from various analytical models are tabulated in Table 5. The total pore volume, the volume of mesoporosity, and the percentage of mesoporosity are calculated as 180.23
shows the presence of small mesopores. The other porosity parameters including Burret-Joyner-Halenda (BJH) pore size distribution, the BET specific surface area (SBET) and the volume of adsorbed gas to form a single layer on the surface under STP condition (Vm) from various analytical models are tabulated in Table 5. The total pore volume, the volume of mesoporosity, and the percentage of mesoporosity are calculated as 180.23 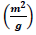 , 132.17
, 132.17 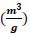 and 73.33%, respectively. The single-layer thickness (t) from t-plot, the peak of the size and mean pore diameter in pore size distribution are calculated as 5.30 nm, 7.62 nm and 2.17 nm, respectively. Table 6 summarizes the characteristics and photodegradation properties of the pure and doped TiO2 NPs. The calculations revealed that the result of X-ray diffraction and physical adsorption-desorption are in good agreement to determine the specific surface area.
and 73.33%, respectively. The single-layer thickness (t) from t-plot, the peak of the size and mean pore diameter in pore size distribution are calculated as 5.30 nm, 7.62 nm and 2.17 nm, respectively. Table 6 summarizes the characteristics and photodegradation properties of the pure and doped TiO2 NPs. The calculations revealed that the result of X-ray diffraction and physical adsorption-desorption are in good agreement to determine the specific surface area.
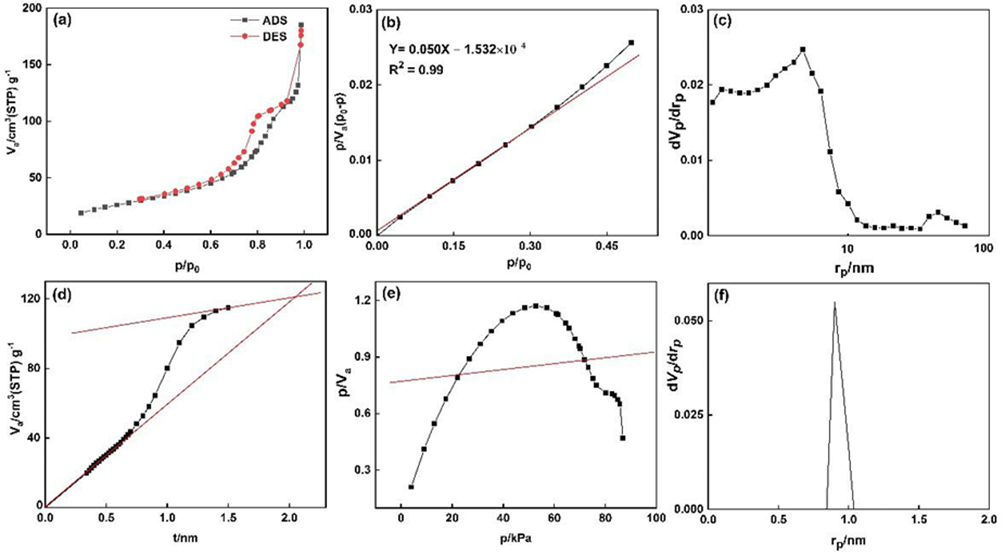
Fig. 10
(a) N2 adsorption-desorption isotherm, (b) BET plot, (c) BJH plot, (d) t-plot, (e) Langmuir, (f) MP-plot of doped TiO2 Nps.
N2 physisorption data of doped TiO2 Nps.
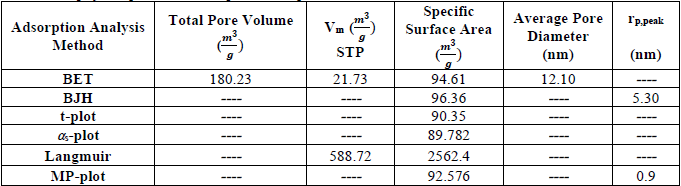
Summary of specifications and photodegradation properties of the pure and doped TiO2 NPs.
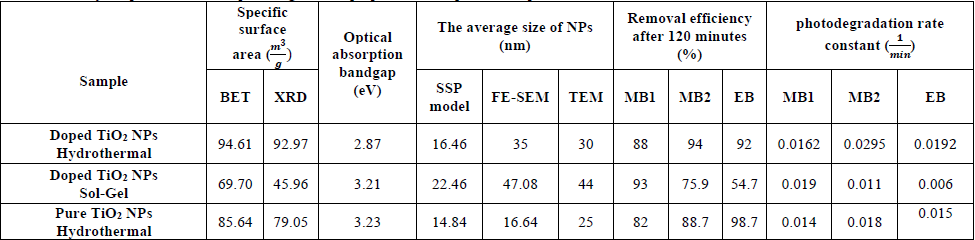
According to Table 6, BET and XRD analyses reveal the specific surface area of doped NPs is higher than the pure and doped NPs in the sol -gel synthesis method, while the optical absorption bandgap of doped NPs in the hydrothermal method is the lowest. The SSP, TEM and FE-SEM techniques show that the size of doped particles in the sol-gel method has the highest value. The results represent the highest removal efficiency and the photodegradation rate of MB1, MB2 and EB dyes by doped TiO2 in the hydrothermal method. According to the DRS investigation, the optical bandgap and specific surface area are the most impressive factors affecting the photodegradation of dyes, because the smaller optical bandgap absorbs a lower range of incident photon energies and causes more degradation of dyes, finally.
Conclusion
In summary, doped TiO2 NPs have been successfully synthesized by the hydrothermal method, while the structure, optical bandgap, and photocatalytic activity have been investigated. The X-ray diffraction technique indicated the tetragonal anatase crystalline phase of NPs. The broadening of XRD peaks is separately influenced by the strain and the size effects, furthermore investigated by two analysis methods i.e., W- H and H-W. These methods, including various models (UDM, USDM, UDEDM and SSP) that are different in the isotropic and homogenous nature, are utilized to calculate the lattice strain-stress parameters. The obtained results have revealed that the SSP model had the least data scattering around the linear fit plot and was the most appropriate model to determine the structural parameters. The size and morphology of the doped TiO2 NPs were determined by the SEM and TEM images to be about 30 to 35 nm. The physical surface, Porosity, layer thickness, pore size distribution and porosity of the doped TiO2 NPs were estimated by the N2 adsorption-desorption. Textile contaminant dyes, including MB1, MB2 and EB were utilized to measure the photocatalytic activity of the doped TiO2 NPs by photodegradation of dyes under UV-Vis irradiation1. The photocatalytic activity rate was calculated for MB1, MB2 and EB to be 0.0162, 0.0295 and 0.0192 , respectively. The chemical bonds and the vibration modes of doped TiO2 NPs were investigated by the FTIR. The optical bandgap of synthesized doped TiO2 NPs was calculated to be 2.87 eV. The results of the XRD on the size and Specific surface area were completely consistent with the results of the performed techniques. The specific surface area of doped NPs was higher than the pure and doped NPs in the sol-gel synthesis method. The results illustrated the highest removal efficiency and the photodegradation rate of MB1, MB2 and EB dyes by doped TiO2 in the hydrothermal method. The results demonstrated that the dopants, bandgap and specific surface area play a key role to control the photodegradation rate and photocatalytic performance of the TiO2 NPs.
Acknowledgments
The authors appreciate University of Kashan and Islamic Azad University, Tonekabon Branch for their financial support throughout this research project.
References
1. Li, Z.; Yu, L.; Wang H.; Yang, H.; Ma, H. Nanomaterial., 2020, 10, 631-645.
2. Mufti, N.; Laila, IK.; Fuad, A. Int. J. Phys.: Conf. Ser. 2017, 853, 012035.
3. Naik, K.M.; Higuchi, E.; Inoue, H. J. Power Sources. 2020, 455, 227972-227986.
4. Karim, M.R.; Alam, M.M.; Aijaz, M.O.; Asiri, A.M.; AlMubaddel, F.S.; Rahman, M.M. RSC Advances. 2020, 10,12224-12233.
5. Fagan, R.; Mc Cormack, D.E.; Dionysiou, D.D.; Pillai, S.C. Mater. Sci. Semicond. Process. 2016, 1 42, 2-14.
6. Zolfaghari, A.; Riazian, M.; Ashjari, M. Res. Chem. Intermed. 2021,47, 1809-1828.
7. Li, D.; Song, H.; Meng, X.; Shen, T.; Sun, J.; Han, W.; Wang, X. Nanomaterials. 2020, 10, 546-553.
8. Bahmanrokh, G.; Cazorla, C.; Mofarah, S.S.; Shahmiri, R.; Yao, Y.; Ismail, I.; Chen, W.F.; Koshy, P.; Sorrell, C.C. Nanoscale. 2020, 12, 4916-4934.
9. Farner, J.M.; De Tommaso, J.; Mantel, H.; Cheong, R.S.; Tufenkji, N. Environ. Sci.: Nano. 2020, 7,1781-1793.
10. Ziental, D.; Czarczynska-Goslinska, B.; Mlynarczyk, D.T.; Glowacka-Sobotta A.; Stanisz, B.; Goslinski, T.; Sobotta, L. Nanomaterials. 2020, 10, 387-399.
11. Mugundan, S.; Rajamannan, B.; Viruthagiri, G.; Shanmugam, N.; Gobi, R.; Praveen, P. Appl. Nanosci. 2015, 5, 449-456.
12. Najafi, F.; Faraji, M.; Marjani, A.P. J.Mex. Chem. Soc. 2019, 63,169-179.
13. Cruz-González, N.; Calzadilla, O.; Roque, J.; Chalé-Lara, F.; Olarte, J.K.; Meléndez-Lira, M.; Zapta-Torres, M. Int. J. Photoenergy. 2020, 7, 1-10.
14. Pirsaheb, M.; Hossaini, H.; Nasseri, S.; Azizi, N.; Shahmoradi, B.; Khosravi, T. J. Nanostruct. Chem. 2020, 19, 1-7.
15. Rotich, J.; Mwamburi, M.; Walter, N.; Maghanga, C.; Munyati, O.; Hatwaambo, S. Mater. Res. Express. 2020, 7, 25505-22215.
16. Sadeghzadeh-Attar, A. J. Asian Ceramic Societies. 2020, 8, 662-676.
17. Khairy, M.; Zakaria, W. Egypt. J. Pet. 2014, 23, 419-426.
18. Choi, A.Y.; Han, C.H. J. Nanosci. Nanotech. 2014, 14, 8070-8073.
19. Zhang, F.; Wang, X.; Liu, H.; Liu, C.; Wan, Y.; Long, Y.; Cai, Z. Appl. Sci. 2019, 9, 2489-2496.
20. Al-Jitan S.; Palmisano, G.; Garlisi, C. Catalysts. 2020, 10, 227-238.
21. Mathew, S.; Ganguly, P.; Rhatigan, S.; Kumaravel, V.; Byrne, C.; Hinder, S.J.'; Bartlett, J.; Nolan, M.; Pillai, S.C. Appl. Sci . 2018, 8, 2067-2074.
22. Zhu, X.; Pei, L.; Zhu, R.; Jiao, Y.; Tang, R.; Feng, W. Sci. Rep. 2018, 8, 1-4.
23. Wang, R.; Shen, J.; Zhang, W.; Liu, Q.; Zhang, M.; Tang, H. Ceram. Int. 2020, 46, 23-30.
24. Li, Y.; Zhang, L.; Yu, L.; Li, D.; Meng, H.; Ai, Q.; Hu, J.; Jin, L.; Gao, J.; Liu, G. Ceram. Int . 2020, 46, 8-16.
25. Phromma, S.; Wutikhun, T.; Kasamechonchung, P.; Eksangsri, T.; Sapcharoenkun, C. Appl. Sci . 2020, 10, 993-998.
26. Sun, Q.; Li, K.; Wu, S.; Han, B.; Sui, L.; Dong, L. New J. Chem. 2020, 44, 1942-1952.
27. Li. D.; Song, H.; Meng, X; Shen, T.; Sun, J.; Han, W.; Wang, X. Nanomaterials. 2020, 10, 546-552.
28. Cerro-Prada, E.; García-Salgado, S.; Quijano, M.; Varela, F. Nanomaterials. 2019, 9, 26-32.
29. Mushtaq, K.; Saeed, M.; Gul, W.; Munir, M; Firdous, A.; Yousaf, T.; Khan K.; Sarwar, H.M.; Riaz, M.A.; Zahid, S. Inorg. Nano-Met. Chem. 2020, 14, 1-7.
30. Inaba, R.; Fukahori, T.; Hamamoto, M.; Ohno, T. J. Mol. Catal. A: Chem. 2006, 260, 247-54.
31. Lee, M.S.; Park, S.S.; Lee, G.D.; Ju, C.S.; Hong, S.S. Catal. Today. 2005, 101, 283-290.
32. Zori, M.H. J. Inorg. Organomet. Polym. Mat. 2011, 21, 81-90.
33. Nasi, R.; Esposito, S.; Freyria, F.S.; Armandi, M.; Gadhi, T.A; Hernandez, S.; Rivolo, P.; Ditaranto, N.; Bonelli, B. Materials. 2019, 12, 937-942.
34. Lassoued, M.S.; Lassoued, A.; Ammar, S.; Gadri, A.; Salah, A.B.; García-Granda, S. J. Mater. Sci.: Mater. Electron. 2018, 29, 8914-8922.
35. Sanchez-Martinez, A.; Koop-Santa, C.; Ceballos-Sanchez, O.; López-Mena, E.R.; González, M.A.; Rangel-Cobián, V.; Orozco-Guareño, E.; García-Guaderrama, M. Mater. Res. Express . 2019, 6, 85085-85091.
36. Vadivel, D.; Branciforti, D.S.; Speltini, A.; Sturini, M.; Bellani, V.; Malaichamy, I.; Dondi, D. Catalysts . 2020, 10, 270-282.
37. Ntozakhe, L.; Taziwa, R.T.; Mungondori, H.H. Mater. Res. Express . 2019, 6, 0850a9.
38. Asadnajafi, S.; Shahidi, S.; Dorranian, D. The Journal of the Textile Institute. 2020, 111, 122-128.
39. Aziz, W.J.; Ali, S.Q.; Jassim, N.Z. Silicon. 2018, 10, 2101-2107.
40. Alotaibi, A.M.; Sathasivam, S.; Williamson, B.A.; Kafizas, A.; Sotelo-Vazquez, C.; Taylor, A.; Scanlon, D.O.; Parkin, I.P. Chem. Mater. 2018, 30, 1353-1361.
41. Méndez-Lozano, N.; Apátiga-Castro, M.; Manzano-Ramírez, A.; Rivera-Muñoz, E.M.; Velázquez-Castillo, R.; Alberto-González, C.; Zamora-Antuñanom M. Results Phys. 2020, 16, 102891-102899.
42. Gholami, M,; Zarei-jelyani, M.; Babaiee, M.; Baktashian, S.; Eqra, R. Ionics. 2020, 26, 4391-4399.
43. Giolli, C.; Rizzi, G.; Scrivani, A.; Ferpozzi, R.; Troglio, S.; Miranda, M.M.; Tolstoguzov, A.; Bardi, U.; Borgioli, F.; Fossati, A.; Credi, la metallurgia italiana. 5th Int. Surf. Eng. Con.(ISEC) Exhibition, Seattle (USA), 2008, 1, 27-36.
44. Aguilar, T.; Carrillo-Berdugo, I.; Gómez-Villarejo, R.; Gallardo, J.J.; Martínez-Merino, P.; Piñero, J.C.; Alcántara, R.; Fernández-Lorenzo, C.; Navas, J.A Nanomaterials. 2018, 8, 816-821.
45. Wang, M.; Chen, C.; Zhao, B.; Zeng, Q.; He, D. Mater. Lett. 2013, 109, 104-107.
46. Kathavate, V.S.; Deshpande, P.P. Surf. Coat. Technol. 2020,11, 125902-125908.
47. Ikraam, M.; Shahid, S.; Zaman, S.; Sarwar, M.N. J. Electron. Mater. 2016, 45, 4228-4236.
48. Billik, P.; Plesch, G.; Brezová, V.; Valko, M.; Mazúr, M. J. Phys. Chem. Solids. 2007, 68, 1112-1116.
49. Khaghani-Dehaghani, M.A.; Ebrahimi-Kahrizsangi, R.; Setoudeh, N.; Nasiri-Tabrizi, B. Int. J. Refract. Met. Hard Mater. 2011, 29, 244-249.
50. Dhahad, H.A.; Ali, S.A.; Chaichan, M.T. Case Studies in Thermal Engineering. 2020, 4, 100651-100661.
51. Pinchuk, V.A.; Kuzmin, A.V. Fuel. 2020, 267, 117220-117229.
52. Moreira. A.J.; Campos, L.O.; Maldi, C.P.; Dias, J.A.; Paris, E.C.; Giraldi, T.R.; Freschi, G.P. Environ. Sci. Pollut. Res. 2020, 27, 27032-27047.
53. Quintero. Y; Mosquera. E.; Diosa, J.; García, A. J. Sol-Gel Sci. Technol. 2020, 5, 1-9.
54. Santhi, K.; Navaneethan, M;; Harish, S.; Ponnusamy, S.; Muthamizhchelvan, C. Appl. Surf. Sci. 2020, 500, 144058-144065.
55. Shojaie, A.; Fattahi, M.; Jorfi, S.; Ghasemi, B. J. Environ. Chem. Eng. 2017, 5, 4564-4572.
56. Riazian, M.; Yousefpoor, M. Int. J. Smart Nano Mater. 2020, 4, 1-8.
57. Beyer, J.; Mamakhel, A.; Søndergaard-Pedersen, F.; Yu, J.; Iversen, B.B. Nanoscale. 2020, 12, 2695-2702.
58. Pawar V, Kumar M, Dubey PK, Singh P. InAIP Conference Proceedings, 2018, 23, 020020.
59. Hamadanian, M.; Reisi-Vanani, A.; Behpour, M.; Esmaeily, A.S. Desalination. 2011, 281, 319-324.
60. Jing, Y.; Mu, X.; Liu, X.; Liu, C. Nucl. Instrum. Methods Phys. Res., Sect. B, 2017, 406, 670-675.
61. Mote, V.D.; Purushotham, Y.; Dole, B.N. Cerâmica. 2013, 59, 614-619.
62. Al‐Tabbakh, A.A.; Karatepe, N.; Al‐Zubaidi, A.B.; Benchaabane, A.; Mahmood, N.B. Int. J. Energy Res. 2019, 43, 1903-1911.
63. Rajender, G.; Giri, P.K. J. Alloys Compd. 2016, 676, 591-600.
64. Fell, C.R.; Qian, D.; Carroll, K.J.; Chi, M.; Jones, J.L.; Meng, Y.S. Chem. Mater . 2013, 25, 1621-1629.
65. Motevalizadeh, L.; Heidary, Z.; Abrishami, M.E. Bull. Mater. Sci. 2014, 37, 397-405.
66. Filippo, E.; Carlucci, C.; Capodilupo, A.L.; Perulli, P.; Conciauro, F.; Corrente, G.A.; Gigli, G.; Ciccarella, G. Mater. Res. 2015, 18, 473-481.
67. Ðorđević, V.; Milićević, B.; Dramićanin, M.D. IntechOpen, 2017, 26, 25-52.
68. Ansari, S.A.; Khan, M.M.; Ansari, M.O.; Cho, M.H. New J. Chem . 2016, 40, 3000-3009.
69. Fischer, K.; Gawel, A.; Rosen, D.; Krause, M.; Abdul, Latif.; A, Griebel J.; Prager, A.; Schulze, A. Catalysts . 2017, 7, 209-316.
70. Chelli, V.R.; Chakraborty, S.; Golder, A.K. J. Mol. Liq. 2018, 271, 380-388.
71. Bezrodna, T.; Puchkovska, G.; Shymanovska, V.; Baran, J.; Ratajczak, H. J. Mol. Struct. 2004, 700,175-181.
72. Erkov, V.G.; Devyatova, S.F.; Molodstova, E.L.; Malsteva, T.V.; Yanovskii, U.A. Appl. Surf. Sci. 2000, 166, 51-56.
73. Wang, X.; Jimmy C.Y.; Liu, P.; Wang, X.; Su, W.; Fu, X. J. Photochem. Photobiol,. A. 2006, 179, 339-347.
Author notes
*Corresponding author: Mehran Riazian, email: m.riazian@toniau.ac.ir, Tel:+989122116905, Fax:+981924271105

 cygnusmind
cygnusmind