Journal of the Mexican Chemical Society, vol. 65, no. 3, 2021
Sociedad Química de México A.C.
Fátima M. Soto-Suárez *
Universidad Nacional Autónoma de México, Mexico
Víctor Duarte-Alaniz
Universidad Nacional Autónoma de México, Mexico
Ramiro F. Quijano-Quiñones
Universidad Autónoma de Yucatán, Mexico
Gabriel Cuevas *
Universidad Nacional Autónoma de México, Mexico
Received: 22 February 2020
Accepted: 21 May 2021
Abstract.: The inversion process of 1,3-cyclohexanedione was studied to know the energy associated with the chair-chair interconversion. 1,3-cyclohexanedione has a conformational inversion energy of 1.87 kcal/mol evaluated at M06-2x/6-311++G(2d,2p) level of theory. The global process combines inversion and topomerization originated by boat-boat interconversion that includes only two trajectories to the inversion transition state but no six-like cyclohexane, or four-like oxane and thiane. The process includes two different twisted boats associated with a boat transition state. A global scheme is proposed to represent this conformational equilibrium.
Keywords: Inversion, topomerization, 1,3-cyclohanedione, conformational analysis, transition state.
Resumen.: Se estudió el proceso de inversión de la 1,3-ciclohexanediona para conocer la energía asociada a la interconversión silla-silla. La 1,3-ciclohexanediona tiene una energía de inversión conformacional de 1.87 kcal/mol evaluada al nivel de teoría M06-2x/6-311++G(2d,2p). El proceso global combina la inversión y la topomerización originada por la interconversion entre dos confórmeros de bote, que incluye sólo dos trayectorias que conectan con el estado de transición de inversión, a diferencia del ciclohexano que tiene seis, y el oxano y el tiano que cuentan con cuatro. El proceso incluye dos estructuras de botes torcido diferentes asociados a un estado de transición de bote. Se propone un esquema global para representar este equilibrio conformacional.
Palabras clave: Inversión, topomerización, 1,3-ciclohexanodiona, análisis conformacional, estado de transición.
Introduction
The isolation and structural characterization of riolozatrione,[1] (1, Scheme 1), a compound that exhibits moderate activity in vitro against herpes simplex virus [2] has aroused interest in the study of the conformational dynamics of substituted 1,3-cyclohexanodione. In this compound, a quaternary stereogenic center is present at position 9 and is formed by the combination of a methyl group and the trans-2,5-dimethyl-3,4,5,6-tetrahydropentalene-1(2H)-one (CPLN). The dimethyl-cyclopropane group anchors the conformation, so the axial arrangement of the cyclopentalenone group is defined during the biosynthesis process. Because the cyclopropane ring is conjugated to the carbonyl group, it is possible to open it employing a suitable nucleophilic attack, making it possible to have conformationally active 2,2-disubstituted-1,3-diketones (ax eq, Scheme 1).
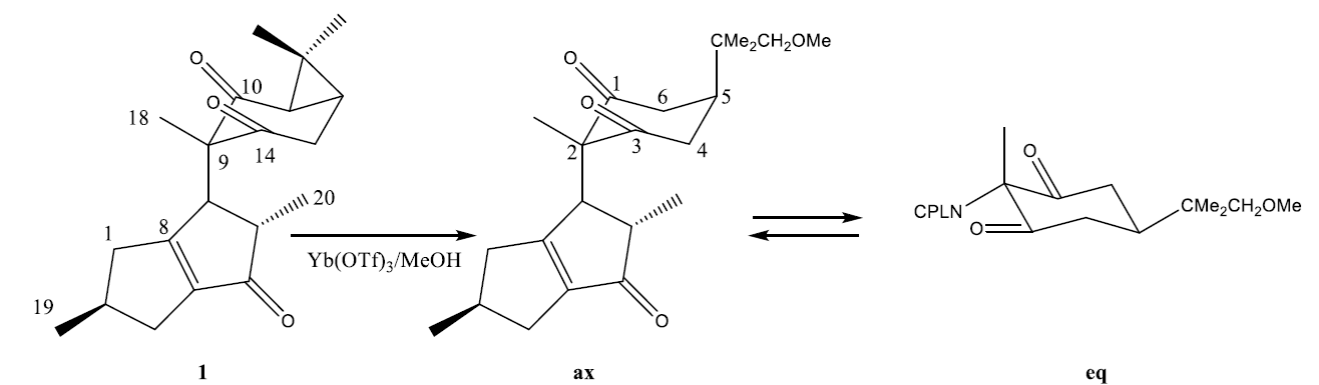
Scheme 1
Riolozatrione (1) and the conformational equilibrium of its methoxylated derivative.
The study of the different arrangements that a molecule could present due to the rotation of single bonds is the subject of conformational analysis. It is known that the inversion process is that in which one chair-type conformer is interchanged with another, causing that the substituents occupying axial positions in the first one, pass to equatorial positions in the other and vice versa. This is called chair-chair interconversion. (Scheme 2).
Scheme 2
Chair-chair interconversion of cyclohexane.
In principle, a single bond can have an infinite number of arrangements, but these are associated with the energy so that only the minimum energy stationary states or an average of them are experimentally observable. From the formal point of view, the other stationary states that can be studied are conformational transition states. Fig. 1 shows the global inversion scheme of oxane (oxacyclohexane). The study of the conformational properties of the basic nucleus provides information that can be extended to other systems, as demonstrated by the study of oxane, thiane, [3] and methyl-clcyclohexane,[4] examples with which it has been possible to establish the need to modify the traditional schemes used to explain the conformational processes in six-membered rings, in which it is not clear that the inversion process is linked to the topomerization process.5
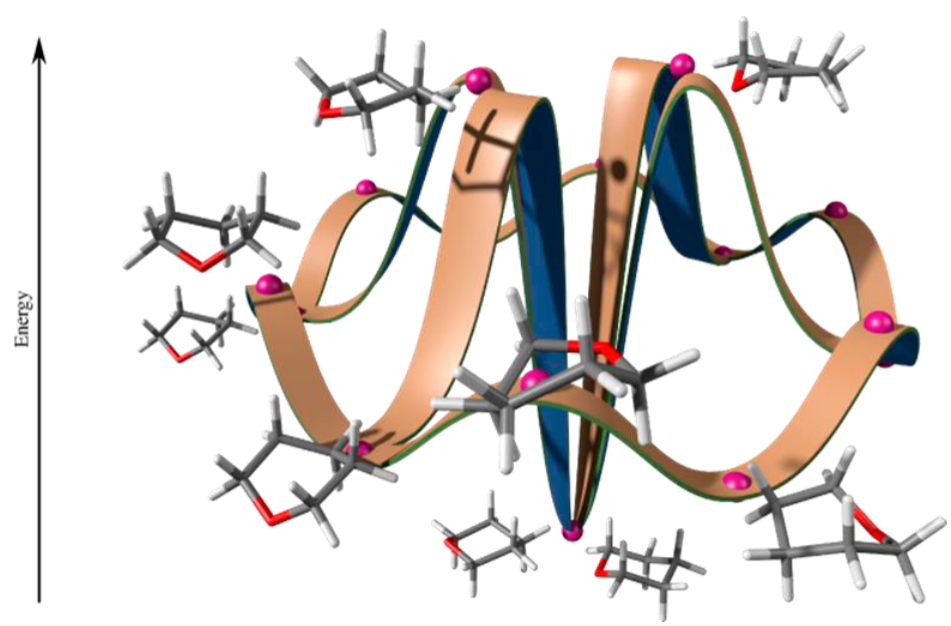
Fig. 1
Global inversion scheme of oxane.
As can be seen, the inversion process allows the exchange between a chair conformer and a twisted boat, (Fig. 1) which happens through a transition state in which five heavy atoms are located practically in the same plane. In this step, there is the highest barrier, which is in the order of 10 kcal/mol. This twisted boat is in turn part of the topomerization process, formed by a succession of twisted boats interconnected through boat transition states, conformers where the eclipsing is maximal. Small barriers are associated with boat-boat interchange, and only some boats are interconnected with transition states which allows inversion. For example, the inversion of the cyclohexane is represented by a similar scheme. In that case, all the twisted boats allow exchanging with the transition state leading to one of the two possible chairs. This scheme presents a perspective of the combined processes of inversion and topomerization and shows the points at which they are connected.
It also shows that it is different twisted-boat conformers that lead to the different chairs so that the oversimplified schemes used to illustrate these processes are not rigorous. [5-7]
Returning to the main problem here studied, 1,3-dicarbonyl compounds with hydrogen atoms at position 2 are in equilibrium with the corresponding 3-hydroxy-enones, with different magnitudes of the equilibrium constant, showing dependence on the nature of the ring substituents, the solvent, the concentration, and self-association capability. (Scheme 3) [8] This fact has inhibited the study of the conformational process of this basic ring, as it generates new pathways for inversion and complicates the study of the conformational process.

Scheme 3
Enolization and conformational equilibria in 1,3-ciclohexanedione.
From this information, interest arises in establishing the energy requirements associated with the inversion process of the basic nucleus of 1,3-cyclohexanedione, to establish the experimental conditions in which it is possible to carry out spectroscopic studies. The conformational studies of 6-membered rings are abundant compared to that of rings of other sizes. This is because the inversion energy of six-membered rings is approximately 10 kcal/mol, allowing them to be studied at temperatures close to -90 °C at 1 atm, a temperature accessible with liquid nitrogen. It is known that the study of smaller barriers, of the order of 3 kcal/mol, requires temperatures of the order of -160°C. [9]
It was not until 2003 that a general interest appeared in rigorously addressing inversion processes, as it was necessary to describe the energy associated with the deformation that pyranose rings experienced when interacting with enzymes that recognize and metabolize carbohydrates [10]. It was also necessary to know the effect of conformational exchange in the recognition of molecules involved in different biological processes.[11]
n the other hand, the conformational studies are part of the molecular characterization that is important from the physicochemical point of view, since it allows not only to know the energy associated with the conformation,[12] but also to estimate, among other properties, [13] its effect on the variation of the molar volume. [14]
Cyclohexane is a reference molecule in organic chemistry, so quantitative knowledge of the vapor phase inversion path is relevant, especially for spectroscopic studies. [15] Different stereoisomers of methyl-cyclohexane have been used to evaluate the performance of computational methodologies to reproduce experimental spectra. [16, 17] In these studies it was possible to stablish the stability of conformers [18] and study reaction mechanism, for example, the combustion reaction, specifically in the determination of the migratory aptitude of different types of hydrogen atoms. [19-22]
Some work has focused on the study of the rigorous mechanism of inversion-topomerization of substituted cyclohexanoanes,[23] both processes by the introduction of heteroatoms into the ring and by the incorporation of substituents. [24] Finally, this type of study allows us to establish how conformation at enzyme recognition-catalytic centers defines the absolute stereochemistry of natural products. [25-27]
Theoretical methodology
All electronic structure calculations were performed under the Density Functional Theory (DFT) methodology, implemented in Gaussian09 software [28]. All energies were reported with zero-point energy corrections and are not scaled for comparative purposes. The stationary state geometries (reactants, transition states, and products) were optimized using the meta-GGA M06-2X hybrid functional with the 6-311++G(2d,2p). A Pople basis set, which contains divided triple zeta valence and polarization functions on light and heavy atoms was used. M06-2X functional was employed since it has been recommended to study the kinetics and thermochemical properties. [29, 30] All the stationary states were characterized through the determination of the vibrational normal modes, and the reaction path was followed by integrating the intrinsic reaction coordinate [31] as is implemented in the Gaussian suite of programs. For comparison single point calculations at CCSD(T)/6-31+G(d,p)/M06-2X/6-311++G(2d,2p) were performed.
Results and discussion
The conformational process of 1,3-cyclohexanodione was studied at the M06-2X/6-311++G(2d,2p) level where the global minimum corresponds to the chair conformer (S, Fig. 2). Because the molecular geometries of all the steady states presented here are similar to that generally accepted, their comparative analysis will not be discussed here. All atomic coordinates of every conformer are included in the supporting information. In the chair conformer, it is observed that the segment C1C2C3C4 (see Scheme 3 for numbering), which includes the two carbonyl groups, is flattened concerning cyclohexane, with an angle of 44.7°, which can be compared with the opposed segment of the same molecule where the angle C4C5C6C1 is 56°. The planarity of the chair-like conformers leads to a decrease of the inversion activation energy. [32]
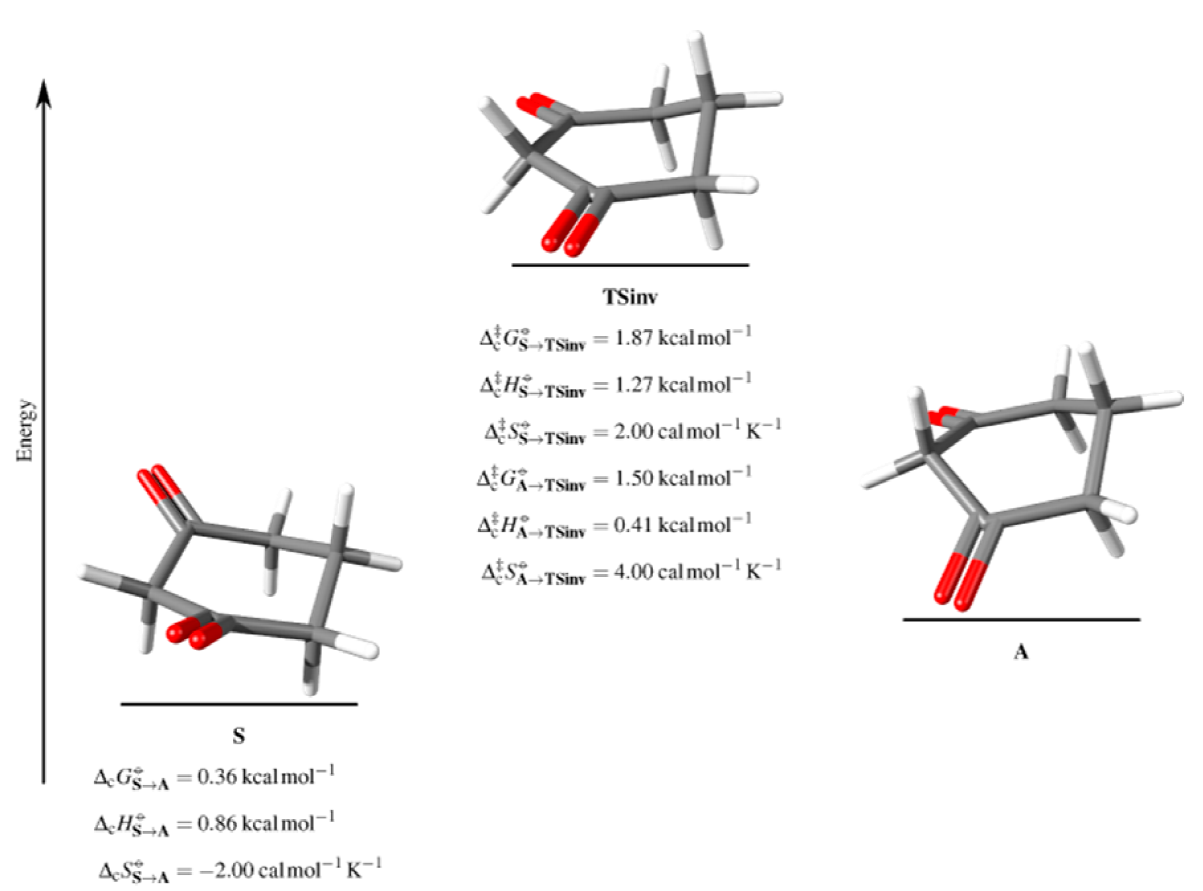
Fig. 2
First elemental step associated with the inversion of 1,3-cyclohexanedione, in which cMº and Δc‡ Mº are the conformational ('c' subindex) standard property M change between two minima or a minimum and a transition state as indicated.
In Fig.2 the inversion step of 1,3-cyclohexanedione is shown, with a barrier of 1.87 kcal/mol, going through a conformational transition state (TSinv), where the segment that includes the two carbonyl groups is completely flattened (C1-C4, τ = 3.3°), producing a sofa topology. A twisted boat (A) is then accessed, just Δc‡ GºA→S = -0.36 kcal/mol less stable than the chair and 1.50 kcal/mol more stable than the transition state. This boat also shows flattening of the C1-C4 segment, with τ = 38.7° (with respect to the 60° of a standard gauche angle) while the C3-C6 segment shows an angle of 53.7°. This conformer is the only one associated with the inversion, which differentiates this process from others such as oxane or thiane [3] that have two sofa transition states or methyl-cyclohexane that has three of them. [4]
This small barrier makes it impossible to freeze the conformational equilibrium to make it observable under liquid nitrogen operating conditions, the infrastructure that is generally available in Mexico. A barrier of this magnitude requires temperatures close to -150°C to be studied.
The only elemental step for topomerization in the 1,3-cyclohexanedione inversion process passes from the twisted boat already referred as A through transition state 2 (Fig. 3), a boat in which one of the carbonyl groups is arranged in front of the methylene of the opposite position in the ring, in one case the position 3 versus 6 or 1 versus 4, pulling carbonyl groups out of the ring plane. In this case, the activation energy is 3.43 kcal/mol, with a change in entropy Δc‡ SºA→2 = -4.00 cal/mol K, which is congruent with a decrease in the molecular freedom degrees characteristic of this kind of transition states. An important difference with respect to other conformational equilibria studied until now is that the higher barrier relates to the topomerization step and not to inversion, which also requires very low temperatures to be experimentally studied.
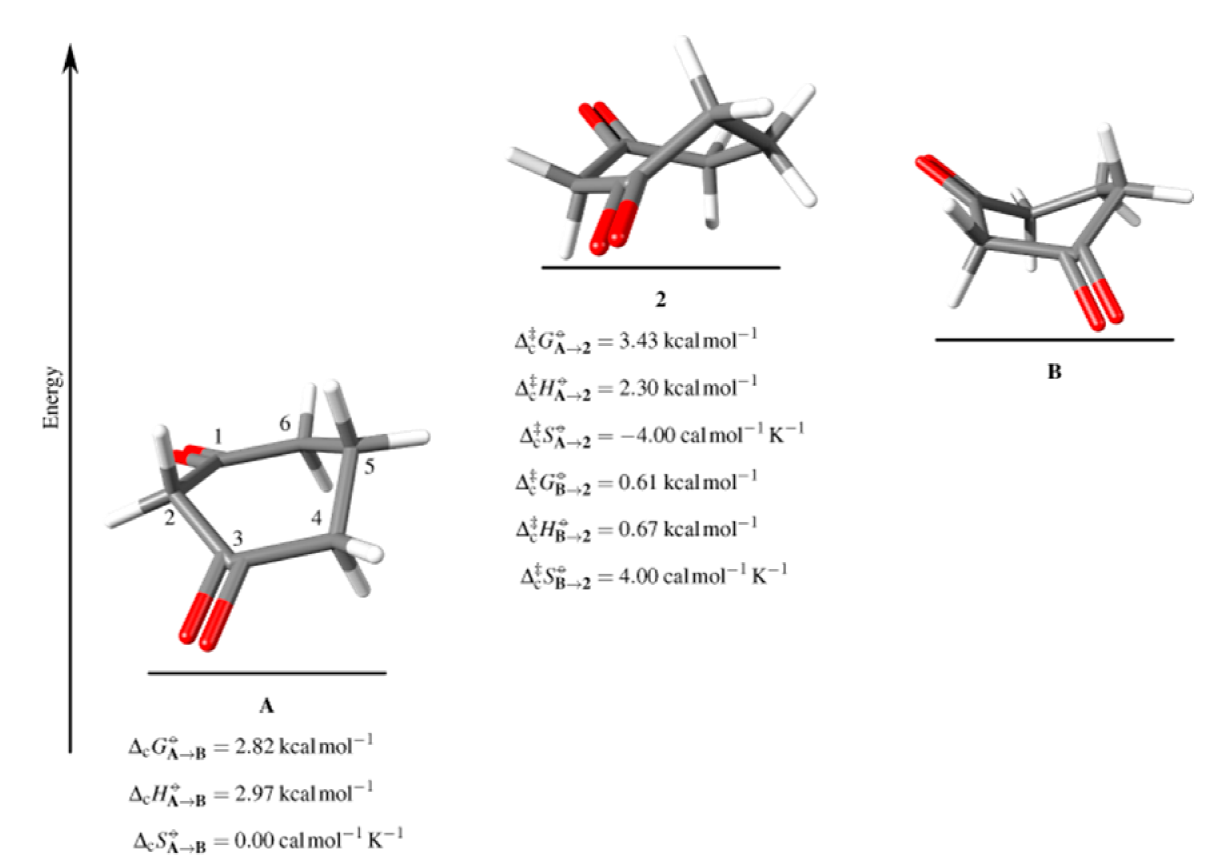
Fig. 3
Topomerization elemental step for the inversion of 1,3-cyclohexanedione. The notation is the same as in Fig. 2.
The twisted boat B shows a conformational free energy that is 0.61 kcal/mol more stable than the transition state, however, the enthalpy contribution to this energy is only 0.67 kcal/mol, which is dominated by an entropic contribution, of -4 cal/K mol which at 298 K means a contribution of 1.19 kcal/mol to free energy.
It is expected that the twisted boat B would be exchanged with their mirror image B’, (Fig. 4) through a transition state as a part of the topomerization process. Careful inspection of the potential energy surface did not allow us to locate a reasonable steady state of transition for this process. Because each functional describes the potential energy surface differently, this step was studied using the functionals B1B95 and MPWB95, in addition to the MP2 method, finding that none of them describes the sought transition state, so the associated elemental step is not part of this process. From this result, it is clear that the exchange between the mirror images B and B’ would occurs throw an elusive transition state as part for example of a very flat surface, or the process occurs without the participation of a transition state.
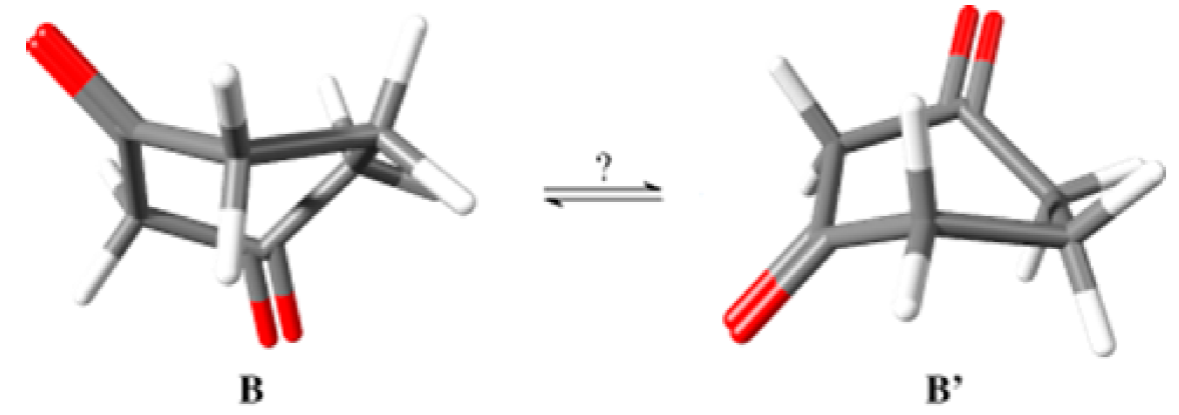
Fig. 4
Topomerization between boats with an undetermined transition state.
If this equilibrium does not occur, the chairs would not exchange, a phenomenon that is known to occur in 2,2,5,5-tetramethyl-1,3-cyclohexanedione [33] and its 2,2-dibenzoylated derivative [34] compounds that fail to show decoalescense of any NMR signals even at -160°C, experimental data that confirm the results presented here.
Thus, the global process is shown in Fig. 5. As it can be seen, there is a single transition state through which the inversion of 1,3-cyclohexanedione occurs, which is also the access of topomerization, which is conducted through four conformational transition states (boats) and its associated minima, twisted boats of two types. Only boats of type A allow access to the inversion transition state, in one case for the starting chair and the other for the inverted one. In this way, it is clear that inversion and topomerization are linked processes that must be represented in the way shown in Fig. 5 and not by traditional schemes, [5-7] in which the inversion and topomerization are described separately or were an undetermined number of boats as are usually described. Perhaps the most important contribution of topomerization to conformational equilibrium is the number of boats and twisted boats generated during the process, degrees of freedom that increase the entropy.
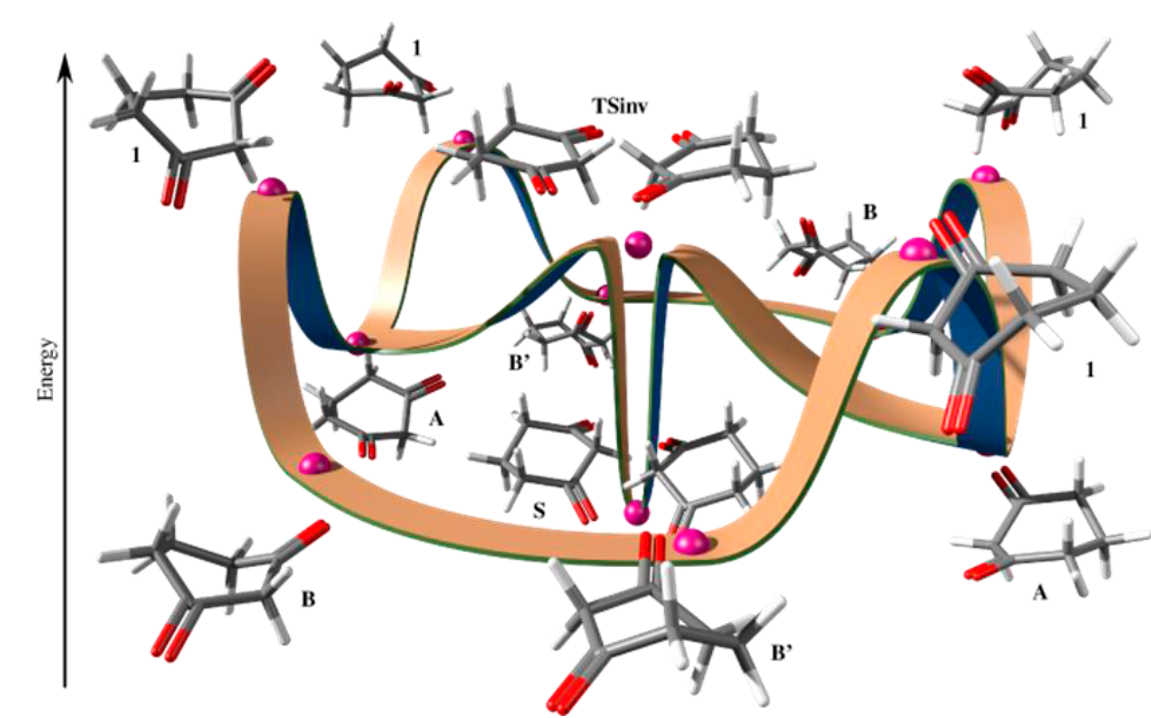
Fig. 5
Global process of inversion of 1,3-cyclohexanedione.
Table 1 shows the electronic energy difference between the chair conformer and the rest of the conformers calculated using single point calculations results obtained by the HF, MP2, MP3, MP4D, MP4SDQ, CCSD and CCSD (T) methods with the 6-31+G(d,p) basis set. The geometry used is the one optimized at the M06-2X/6-311++G(2d,2p) level. As can be seen, except for the Hartree-Fock method, the differences are quite consistent. These data make it possible to verify that the magnitude of the inversion energy is smaller with respect to the topomerization barrier. These results are compatible with those previously obtained for oxane where various calculation methods, including thermochemical methodologies such as G2, show consistency. [3]
Electronic energy differences referred to the S chair conformer calculated with several methods. Values are in kcal/mol.

To evaluate the effect of the substitution in the conformational process, the inversion of 2,2-dimethyl-1,3-cyclohexanedione was also studied. It was possible to locate similar intermediates as in the case of the parent ring. The determined inversion free energy was 3.23 kcal/mol, with topomerization free energy barriers of 0.95 and 1.88 kcal/mol, as shown in Fig. 6. In this case, it was not possible to find a transition state that allowed interconversion between mirror image conformers. Nor was an important effect observed in the topology of the intermediates produced by the gem-substitution at position 2, but a larger inversion energy was determined. [3,4]
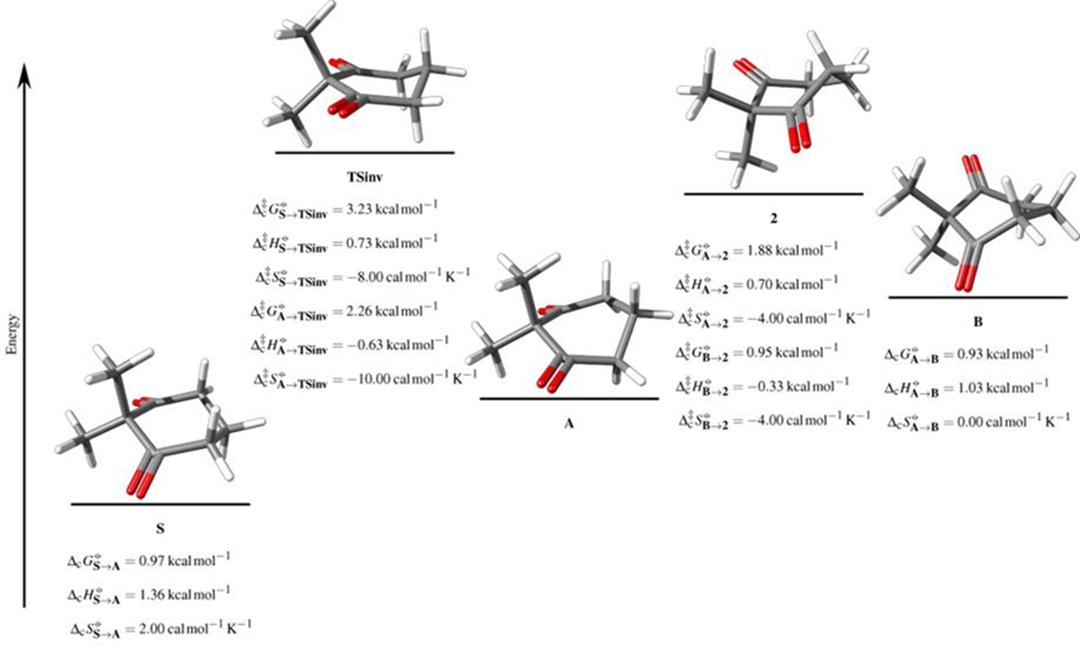
Fig. 6
Stationary states associated with the inversion process of 2,2-dimethyl-1,3-cyclohexanedione.
Conclusion
The 1,3-cyclohexanedione inversion process has a conformational inversion energy of 1.87 kcal/mol and combines inversion and topomerization processes. The whole process includes four transition states of the same type, which includes the interchange of two different boat structures, and an interconversion transition state, as well as seven minima. Without a significant substitution effect in the ring geometry of the intermediates, the 2-gem-dimethyl derivative showed a larger inversion energy of 3.23 kcal/mol with topomerization free energy barriers of 0.95 and 1.88 kcal/mol. The so-called ground state destabilization energy that would decrease the barrier magnitude is not observed in this case. [35]
The conformational process of 1,3-cyclohanedione shows important differences with respect to other studied systems,[3, 4, 20, 23] such as the existence of only two trajectories for the inversion of twisted boats conformers, the inversion barrier has a smaller value with respect to the barrier with which the twisted-boats are exchanged, and also that it has not been possible to locate the transition state related to the interchange of twisted-boats B and B’. Finally, the magnitude of the determined barriers makes it impossible to use NMR to study the conformational equilibrium at temperatures below -160 °C.
Acknowledgments
The authors are grateful to Dirección de Cómputo y de Tecnologías de Información y Comunicación de la Universidad Nacional Autónoma de México, vía Grant LANCAD-UNAM-DGTIC-094, and to Dirección General de Asuntos del Personal Académico (DGAPA) via Grant No. IN-205620. FMSS, is grateful to CONACYT-Mexico for the scholarship granted and to the referees for useful comments.
References
1. Melchor-Martínez, E.M.; Silva-Mares, D.A.; Torres-Lopez, E.; Waksman, N.; Guido, P.; Shao-Nong, Ch.; Niemitz, M.; Sanchez-Castellanos, M.; Toscano, R.; Cuevas, G.; Rivas-Galindo, V.M. J. Nat. Prod. 2017, 80, 2252-2262. DOI: doi.org/10.1021/acs.jnatprod.7b00193.
2. Silva-Mares, D.A.; Torres-Lopez, E.; Rivas-Estilla, A.M.; Cordero-Perez, P.; Waksman, N.; Rivas-Galindo, V.R. Nat. Prod. Commun. 2013, 8, 297-298. DOI: doi.org/10.1177/1934578X1300800305.
3. Fernández-Alonso, M. C.; Asensio, J.L.; Cañada, F.J.; Jiménez-Barbero, J.; Cuevas, G. Chem. Phys. Chem. 2003, 4, 748-753. DOI: doi.org/10.1002/cphc.200200547
4. Fernández-Alonso, M. C.; Cañada, J.; Jiménez-Barbero, J.; Cuevas, G. Chem. Phys. Chem . 2005, 6, 671-681. DOI: doi.org/10.1002/cphc.200400495.
5. Eliel, E.L.; Wilen, S.H. Stereochemistry of organic compounds, Wiley-Interscience, New York, 1994, 689. ISBN: 978-0-471-01670-0.
6. Carey, F.A.; Sundberg, R.J. Advanced Organic Chemistry. Part A. Structure and Mechanisms, Plenium Press, New York. 1990, 132. ISBN: 978-0-387-44899-2.
7. Anslyn, E.V.; Dougherty D.A. Modern Physical Organic Chemistry, University Science Books. Sausalito California 2006, 107. ISBN-13: 978-189138931.
8. Yogev, A.; Mazur, Y. J. Org. Chem. 1967, 32, 2162-2166. DOI: doi.org/10.1021/jo01282a018.
9. Olah, G.A.; Prakash, G.K.S.; Arvanahi, M.; Anet, F.A.L. J. Am. Chem. Soc. 1982, 104, 7105-7108. DOI: doi.org/10.1021/ja00389a037.
10. Biarnés, X.; Nieto, J.; Planas, A.; Rovira, C. J. Biol. Chem. 2006, 281, 1432-1441. DOI: doi.org/10.74/jbc.M507643200.
11. Khodabandeh, M. H.; Rezaeianpour, S.; Davari, M.D.; Sakhaee, N.; Zare, K.; Anary, M.; Naderi, F. J. Theor. Comp. Chem. 2014, 13, 1450047. DOI: doi.org/10.1142/S0219633614500473.
12. Wang, Z. Experimental and kinetic modeling study of cyclohexane and its mono-alkylated derivatives combustion. Springer Thesis. ISBN 978-981-10-5692-5 2018.
13. Bain, A.D.; Baron, M.; Burger, S.K.; Kowalewski, V.J.; Rodríguez M.B. J. Phys. Chem. 2011, 115, 9207-9216. DOI: doi.org/10.1021/jp205375f.
14. Alamairy, M.A.; Benniston, A.C.; Copley, G.; Harriman, A.; Howgego, D. J. Phys. Chem . 2011, 115, 12111-12119. DOI: doi.org/10.1021/jp2070419.
15. Chun, H.J.; Ocola, E.J.; Laane, J. J. Phys. Chem. A. 2016, 120, 7677-7680. DOI: doi.org/10.1021/acs.jpca.6b08727.
16. During, J.R.; Ward, R.M.; Guirgis, G.A.; Gounev. J. Raman- Spectrosc. 2009, 40, 1919-1930. DOI: doi.org/10.1002/jrs.2341.
17. Kuo, C.-M.; Bezuidenhoudt, B.C.B.; Conradie, J. J. Phys. Org. Chem. 2013, 26, 327-334. DOI: doi.org/10.1002/poc.3092.
18. Han, S.; Yoo, H.S.; Ahn, A.-S.; Choi, Y.S.; Kim, S.K. Chem. Phys. Lett. 2011, 518, 38-43. DOI: doi.org/10.1016/j.cplett.2011.11.005.
19. Yao, X. X.; Wang, J.B.; Yao, Q.; Li, Y.Q.; Li, Z.R.¸Li, X.Y. Comb Flam. 2019, 204, 176-188. DOI: doi.org/10.1016/j.combustflame.2019.03.01117.
20. Bian, H.; Wang, A.; Sun, J.; Zhang, F. Proc. Comb. Inst. 2016. 1-8. DOI: doi.org/10.1016/j.proci.2016.07.049.
21. Bian, H.; Ye, L.; Zhong, W. Tetrahedron. 2019, 74, 449-457. DOI: doi.org/10.1016/j.tet.2018.12.020.
22. Bian, H.; Ye, L.; Li, J.; Sun, J.; Liang, T.; Zhong, W.; Zhao, J. Com. Flam. 2019, 205, 193-205. DOI: doi.org/10.1016/j.combustflame.2019.04.024.
23. Bian, H.; Zhang, Y.; Wang, Y.; Zhao, J.; Ruan, X.; Li, J. Int. J. Quantum Chem. 2021, 26636. DOI: doi.org/10.1002/qua.26636.
24. Stortz, C.A. J. Phys. Org. Chem . 2010, 23, 1173-1186. DOI: 10.1002/poc.1689.
25. Barquera-Lozada, J.E.; Cuevas. G. Computational simulation of terminal biogénesis of sesquiterpenes: the case of 8-epiconfertin. In Quantum Biochemistry. Estructure and Biological Activity. Matta Cherif Ed., Wiley-VCH, New York. 2009, 623-650. ISBN: 978-3-527-32322-7.
26. Barquera-Lozada, J.E.; Quiroz-Garcia B.; Quijano, L.; Cuevas, G. J. Org. Chem . 2010, 75, 2139-2146. DOI: doi.org/10.1021/jo902170w.
27. Barquera-Lozada, J.E.; Cuevas, G. J. Org. Chem . 2009, 74, 874-883. DOI: doi.org/10.1021/jo802445n.
28. Frisch, M.J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani G.; Barone, V.; Mennucci, B.; Petersson, G. A.; Nakatsuji, H.; Caricato, M. ; Li, X.; Hratchian, H. P.; Izmaylov, A. F.; Bloino, J.; Zheng, G.; Sonnenberg, J. L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, J. A.; Peralta, J. E.; Ogliaro, F.; Bearpark M.; Heyd, J. J.; Brothers, E.; Kudin, K. N.; Staroverov, V. N.; Keith, T.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, J. M.; Klene, M.; Knox, J. E.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Zakrzewski, V. G.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Dapprich, S.; Daniels, A. D.; Farkas, O.; Foresman, J. B.; Ortiz, J. V.; Cioslowski, J.; Fox, D. J. Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
29. Zhao, Y.; Truhlar, D.G. Acc. Chem. Res. 2008, 41, 157-167. DOI: doi.org/10.1021/ar700111a.
30. Zhao, Y.; Truhlar, D. G. J. Phys. Chem . A. 2008, 112, 1095-1099. DOI: doi.org/10.1021/jp7109127.
31. Fukui, K. Acc. Che. Res. 1981, 14, 363-368. DOI: doi.org/10.1021/ar00072a001.
32. Oki, M. Application of Dynamic NMR Spectroscopy (Methods in Stereochemistry Analysis), Wiley-VCH, 1985. ISBN-13: 978-0895731203
33. Bernard, M.; Canuel, L.; St. Jacques, M. J. Am. Chem. Soc . 1974, 96, 2929-2936. DOI: doi.org/10.1021/ja00816a044.
34. Kwart, H.; Rock, M.C.; Sanchez-Obregon, R.; Walls, F. J. Am. Chem. Soc . 1972, 94, 1759-1760. DOI: doi.org/10.1021/ja00760a064.
35. Anderson, V.E. Ground State Destabilization. In eLS, Ed., Wiley, 2001. DOI: doi.org/10.1038/npg.els.0000625.
Author notes
*Corresponding author: Fátima M. Soto-Suárez, e-mail: famosua88@gmail.com, Gabriel Cuevas, e-mail: gecgb@hotmail.com

 cygnusmind
cygnusmind