Journal of the Mexican Chemical Society, vol. 64, no. 3, 2020
Sociedad Química de México A.C.
Brenda Manzanilla
Universidad de Guanajuato, Mexico
Juvencio Robles *
Universidad de Guanajuato, Mexico
Received: 11 March 2020
Accepted: 22 June 2020
Funding
Funding source: CONACYT
Contract number: 1237332
Contract number: 580068/296892
Abstract: Allotropes of carbon such as graphene, graphane, fluorographene, doped graphene with N, B or P, graphene oxide, graphyne, and graphdiyne were studied through conceptual DFT reactivity descriptor indexes. To understand their chemical behavior and how they interact with different types of molecules, for instance, drugs (due to their potential use in drug carrier applications). This work shows the results of the changes in the global and local reactivity descriptor indexes and geometrical characteristics within the different graphene derivatives and rationalizes how they can interact with small molecules. Molecular hardness, the ionization energy, the electron affinity, electrodonating power index, and electroaccepting power indexes are the computed global reactivity descriptors. While, fukui functions, local softness, and molecular electrostatic potential are the local reactivity descriptors. The results suggest that the hybridization of carbons in the derivatives is kept close to sp3, while for graphene is sp2, the symmetry changes have as consequence changes in their chemical behavior. We found that doping with B or P (one or two atoms doped) and functionalizing with -OH or -COOH groups (as in graphene oxide), decreases the ionization energy in water solvent calculations, allowing for easier electron donation. On the other hand, doping with N atoms and functionalizing with F atoms increases the electron affinity. These types of changes enhance the chemisorption or physisorption by non-covalent interactions and covalent interactions with small molecules, principally, in the carbon atoms nearest to the doped/functionalized atom.
Keywords: Graphene, graphene derivatives, reactivity indexes, electronic structure calculations, conceptual DFT.
Resumen: Los alótropos de carbono como el grafeno, el grafano, el fluorografeno, el grafeno dopado con N, B o P, el óxido de grafeno, el grafino y el grafidiino se estudiaron mediante los índices de los descriptores de reactividad de la DFT conceptual. Ello, para comprender su comportamiento químico y cómo interactúan con diferentes tipos de moléculas, por ejemplo, fármacos (debido a su posible uso en aplicaciones como transportadores de fármacos). Este trabajo muestra los resultados de los cambios en los índices de los descriptores de reactividad global y local y las características geométricas de los diferentes derivados de grafeno y, predice cómo podrián interactuar con moléculas pequeñas. La dureza molecular, la energía de ionización, la afinidad electrónica, el índice de potencia electrodonadora y electroaceptora son los descriptores DFT de reactividad global calculados. Mientras que las funciones de fukui, la suavidad local y el potencial electrostático molecular son los descriptores de reactividad local. Los resultados sugieren que la hibridación de los carbonos en los derivados se mantiene cerca de sp3, mientras que para el grafeno es sp2, los cambios de simetría tienen como consecuencia cambios en su comportamiento químico. Descubrimos que el dopaje con B o P (uno o dos átomos dopados) y la funcionalización con grupos -OH o -COOH (como en el óxido de grafeno), disminuye la energía de ionización en los cálculos de solvente con agua, lo que permite una donación de electrones más fácil. Por otro lado, el dopaje con átomos de N y la funcionalización con átomos de F aumenta la afinidad electrónica. Estos tipos de cambios mejoran la quimisorción o fisisorción por interacciones no covalentes e interacciones covalentes con moléculas pequeñas, principalmente en los átomos de carbono más cercanos al átomo dopado/funcionalizado.
Palabras clave: Grafeno, derivados de grafeno, indices de la reactividad, calculos de estructura electronica, DFT conceptual.
Introduction
Two-dimensional allotropes of carbon are materials that have been used for their interesting properties and their ability to form diverse sp, sp2, and sp3 bonds [1]. Graphene (G) and graph-n-yne are 2D materials that have been widely studied [2-5]. Graphene is a material that was discovered by Andre Gaim and Konstantin Novoselov in 2004 by the exfoliation method; graphene consists of a hexagonal (honeycomb) lattice of covalently bound sp2 carbon atoms (Fig. 1) [6,7]. Graph-n-yne is a carbon material proposed by Baughman et al. in 1987 with sp and sp2 hybridized carbon atoms, this means that honeycombs are joined together by acetylenic links (-C≡C-), these can be varied to obtain graphyne, graphdiyne, and so on (Fig. 1) [8-10]. These molecules can suffer a few modifications to enhance their solubility and electronic properties through doping or by functionalization. Doped graphene involves replacing one atom of carbon by one heteroatom, usually N, B, or P [11-14]. Functionalizing graphene adds an atom or chemical group to a carbon atom of graphene. A few examples are graphane, fluorographene and graphene oxide [12,15,16]. In graphane all the carbon atoms are attached to hydrogen atoms; in fluorographene, their carbon atoms are fully joined with fluor atoms; and graphene oxide has a mixed structure containing various functional groups like the epoxy (>O), hydroxyl (-OH), carbonyl (C=O) and carboxyl (-COOH) groups [16]. Therefore, graphane and fluorographene consist of a single layer with sp3 hybridization. Similarly, graphene oxide has sp3 hybridization close to each functionalized carbon atom.
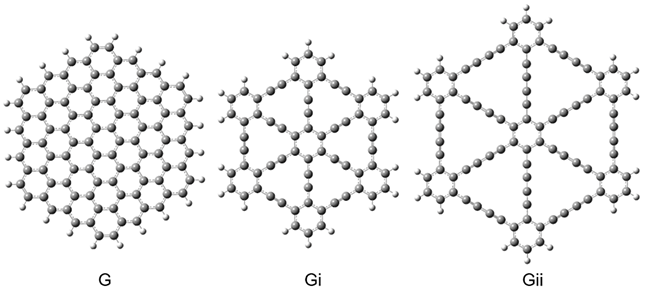
Fig. 1
Optimized finite models at M06-L/6-31G(d) level of theory: graphene (C96H24), graphyne (C66H18), and graphdiyne (C90H18).
Different properties have been attributed to these materials. Graphene has good electrical, thermal properties, large surface area, and biocompatibility [17]. Graphene has been used in a broad range of applications such as energy research, catalysis, and engineering of nanocomposites, and biomaterials, i.e., biosensors and nanocarriers for drug delivery [18]. Graphyne has been used in industry as membrane separator [19]. Graphdiyne has been used in energy storage applications [20]. Doped graphene has been reported for its use in hydrogen storage, in catalysis, in batteries, like supercapacitor, and so on [11,21]. On the other hand, graphane and fluorographene have potential applications in hydrogen storage, for biosensing, supercapacitors, and in biological applications [21-23]. Finally, graphene oxide has been used in biosensors, drug delivery, tissue engineering, antibacterial, and biomedical imaging [16].
Some computational works have been made to understand and predict the chemical behavior of some of these materials. Density Functional Theory (DFT) has been used to understand and rationalize the reactivity and electronic structure of some 2D materials. Conceptual density functional theory (CDFT) allows quantifying the reactivity of a system by local and global reactivity descriptors [19]. Cortes-Arriagada used global reactivity indexes as molecular hardness and electrophilicity and local reactivity indexes as fukui functions to understand the chemistry of graphene oxide and doped graphene. He found that the electrophilic and nucleophilic character of these systems increases by doping them with N or B atoms and functionalizing graphene with hydroxyl groups, so the chemisorption in graphene is favored [20]. Another similar work to investigate the site selectivity of B and/or N doped graphene and graphene oxide by local and global reactivity descriptors found identical results [21]. Whereas, for graphane, graphyne, fluorographene, and graphdiyne, there are no related works reported. In this sense, we performed a DFT study of graphene, graphane, fluorographene, doped graphene with N, B or P, graphene oxide with different functional groups, graphyne, and graphdiyne using global and local reactivity indexes to understand their chemical properties.
Moreover, we have studied the effect of solvent, namely water, because these materials may be used in biomedical applications. Thus, we consider the structure, global descriptors, local descriptors of conceptual DFT, and we use molecular electrostatic maps (MEP) to determine reactive sites. We took a finite model for graphene (C96H24), (Fig. 1), as a reference to compare the change of the descriptors' values and geometrical parameters in the new materials. This finite model is clearly better suited to represent the experimental finite graphene flakes rather than the infinite (extended) graphene flakes which due to a non-zero gap exhibit reactivity not displayed in the extended graphene (gapless) and therefore are often used in a number of chemical and biological applications, such as biosensors, drug nanocarriers [22].
Conceptual DFT: reactivity descriptors
To understand the reactivity of these systems, we computed the following CDFT global reactivity descriptors [19]. The chemical potential (μ) / electronegativity (X), measures the electrons’ tendency to escape/ be attracted from the system. They were obtained by,
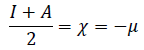 (1)
(1)where the vertical ionization energy (I) and the electron affinity (A): I measures the unrelaxed energy required to remove an electron from the neutral system ground state, and A measures the energy when a neutral system in its ground state captures an electron [23,24]. Both are calculated by,
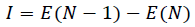 (2)
(2)
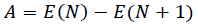 (3)
(3)Then, it is necessary to have single point calculations of cationic (N-1) and anionic (N+1) molecules, at the optimized neutral structure.
Chemical hardness (η) measures the resistance of a molecule to intramolecular charge transfer; then, it is a descriptor that indicates how stable a molecular system is [25]. On the other hand, global chemical softness (S) is the reciprocal of hardness, and it measures the propensity of a system to react. Both are calculated as follows,
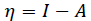 (4)
(4)
 (5)
(5)Electrophilicity index (ω) measures the stabilization energy when a system attracts electronic charge [26]. To measure the response of the system for the subtraction and/or addition of charge was developed the electrodonating power index (ω-) and the electroaccepting power index (ω+) [27]. ω- and ω+ can be approximated as follows,
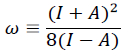 (6)
(6)
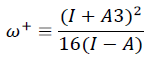 (7)
(7)
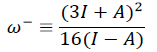 (8)
(8)These indexes are called global reactivity descriptors. Nevertheless, to explain the site selectivity in a molecule, it is necessary to use local reactivity descriptors. The most widely used local descriptor is the fukui function [26]. There are integrated or condensed fukui functions. One is the case of the system adding an electron and another one to remove an electron from the molecule. They were obtained by,
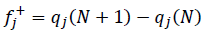 (9)
(9)
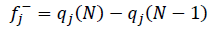 (10)
(10)where the fj is the condensed fukui function, and qj (N) denotes the electronic population or atomic charge of the jth atom
of the reference system [28]. Consequently,
it is necessary to calculate charges of the neutral, cationic, and anionic systems.
Fukui function is an intramolecular local reactivity index. On the other hand, local
softness has also been proposed to analyze possible interactions with electrophile
or nucleophile molecules. It is an intermolecular reactivity index, and it is
possible to compare it with the local values of other units. It is defined as the
product of the total softness times the condensed fukui function [29]. One can obtain 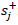 for studies of nucleophilic attacks and
for studies of nucleophilic attacks and 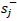 for studies of electrophilic attacks,
for studies of electrophilic attacks,
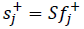 (11)
(11)
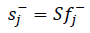 (12)
(12)Computational details
DFT calculations have been performed with the Gaussian 09 software package [30]. Geometry optimizations were carried out using the M06-L functional with the 6-31G(d) basis set [31,32]. All the geometries were found to be minima in the potential energy surface confirmed by the absence of imaginary frequencies in the hessian matrix. A previous conformational search was done with the PM3 semi-empirical method [39,40] and the bpv86/6-31G basis [41-43]. Condensed fukui functions were computed from Hirschfeld charges [33]. Also, we evaluated the effect of the solvent employing the Polarizable Continuum Model (PCM) to mimic water (with ε= 78.36) [34].
We employed a finite model graphene system where carbon atoms were arranged in a hexagonal lattice with borders saturated by hydrogen atoms to eliminate the dangling bonds. We selected the C96H24 size to model graphene with zigzag edges. This model was chosen according to some theoretical studies that have mentioned that symmetric flakes are more stable [35-38]. We evaluated two finite models, i.e., C54H18 and C96H24. Both models were compared with crystallographic data (see SI, supporting information, Table S1). Then, we calibrated C54H18 and C96H24 with various functionals and basis sets to find out the best level of theory for these finite models. The M06-L/6-31G(d) level of theory turned out to be the best in performance/computational cost. On the other hand, graphyne (Gi) and graphdiyne (Gii) were modeled as γ-graph-n-yne finite systems such as C66H18 and C90H18, respectively, Fig. 1. We decided to study the γ-model due to its electronic similarity to G, and with a circular shape [39].
Results and discussion
We studied the effect of doping and functionalization of graphene. Firstly, we doped graphene with one atom of B, N, or P (labeled GB, GN, and GP, respectively), after that, we doped G with two atoms (G2B, G2N, and G2P). Secondly, to model graphane and fluorographene, G was functionalized step-by-step, i.e., we added 1, 2, 4, 6, 24, and 54 H or F atoms. They were tagged like G-1(H or F) when one atom was added, G-2(H or F) when two atoms were added; G-4(H or F) when four atoms were added. For 6, 24, and 54 atoms added, the rings labeled as R1, R3, and R5, shown in Fig. 2, were fully functionalized, so we have: G-(H or F)R1 when six atoms were added; G-(H or F)R3 when 24 atoms were added and G-(H or F)R5 when 54 atoms were added. Graphene oxide was modeled considering models with one -OH, -COOH, >O group, or the presence of all these groups. So, we have the following models: G with one -OH group (G-OH), G with one -COOH group (G-COOH), G with one >O group (G-O). For the mixed groups we have G with two -OH groups (G-A); G with one -OH group and one -COOH group (G-B); G with one -OH and one >O group (G-C); G with two -OH groups, i.e., G-A, with one >O group (G-D). And to have a full model of graphene oxide, G-D was functionalized with one further -COOH group (G-F).
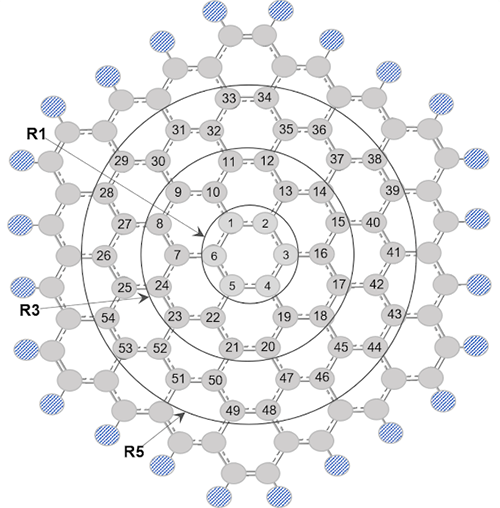
Fig. 2
Labels used for each atom at our finite graphene model (G, C96H24).
We consider the following: for one atom doped or attached; we decided to replace/attach the carbon C3 atom at ring A0, see Fig. 2. Thereafter, for two or more atoms doped or attached, we tested the local reactivity at several sites in G to determine the most useful sites for doping or functionalizing the next atoms. The first step was to make a mixture of different positions, see the places tested in Fig. S10 in the SI. The second step was to determine from the values of condensed fukui functions the most viable positions (see SI, figures S6-S10).
Some of the systems modeled are open-shell due to an unpaired electron configuration. Therefore, some models of doped graphene and graphene oxide are open shells (they are indicated with an *).
Structural properties
First, to understand the changes produced by the chemical modifications in G, we analyze the variation of structural properties such as the variation in C-C distances, C-C-C angles, and hybridization. For models of doped graphene with only one atom doped, we check the distances change in the C-N, C-B, and C-P bonds, i.e., C3-C16, C3-C2, and C3-C4 distances (Fig. 2). These distances increased by 0.21 Å in comparison to C-C distances in G (1.42 Å), (Fig. S1). Analyzing the C2-C3-C16, C4-C3-C16 angles (Fig. 2), they increase by 57.3° in these models compared to the angles in G (i.e., 120º), i.e., they have an intermediate behavior between the sp2 and sp3 hybridization. G doped with two atoms displays a similar behavior as when doped with only one atom. As one can see, significative structural changes are observed in graphene models doped with the P atom.
When we functionalized G with hydrogen and fluor atoms, the C-C distances, in G, increased by 0.10 Å, in the average, when the number of added atoms increases. When G has 54 H/or F atoms attached, the planar structure is wholly lost; see Figures S2 and S3. As a result, these systems lost their sp2 hybridization in the C-C bonds, and they attain pyramidalized bonds in the modified sites. In these models, an antiperiplanar conformation (anti or trans conformation) is preferred for the attached atoms, see Figures S2 and S3. The antiperiplanar conformer is the lowest in energy, see positions tested in Fig. S10. This conformation was selected after having tested different places.
In graphene oxide models, the C3-C16, C3-C2, and C3-C4 distances also increase (from 1.46 to 1.51 Å) and the resulting hybridization, in most systems, is between sp2 and sp3. In Fig. S4, the functional groups have an antiperiplanar conformation, and the oxygen atoms of -OH groups are oriented to the middle of the ring, probably due to an OH-π interaction. These models were the result of having tried different positions, see Fig. S10. In the final models (conformers obtained at the global PES minima), we found hydrogen bonds. We found one weak hydrogen bond in G-COOH between the H atom of -COOH group and the C16 atom in G. G-B has two strong hydrogen bonds, one is between H atom of -COOH group and the C16 atom, and the second one is between =O atom of -COOH group and H atom of the OH group. Finally, G-F has one strong hydrogen bond between the H atom of -COOH group and the O atom of the neighboring -OH group, see Fig. S5.
We also analyzed the C-C bonds in Gi and Gii; they attain an sp2 and sp hybridizations, which have distance values of 1.41-1.42 Å for sp2 bond and 1.22 Å for sp bond. Some reports discuss the bond lengths of these types of systems, and they find dependency on the value of the distances with the functional and basis set employed. Other reports inform bond lengths values in good agreement to experimental data; we have similar values [9]. In water solvent calculations, we found that all distances and angles do not change compared with their values in the gas phase.
Global descriptors
The chemical modifications made to graphene change its chemical behavior, as can be seen in the global descriptors. We compare the values for each descriptor in every system with the ones in the pristine G model. First, we can see that the species with the lower value of I are GP>G2P>G-A>GN>G2N>G-HR5>G-1H>G-F>G-COOH>G-C>G-OH and those with the lower value of I in water phase are G-A>G2P>GP>GB>G2B>G-HR5>G-1H>G-F>G-COOH>G-C>G-HR1>G-OH, see Figures 3(a), 4(a), and Tables S2, and S3. Therefore, for these species, it is easier to remove one electron than for the G model, especially graphene doped with P or B, some models of graphane, and oxide graphene models with -COOH and -OH groups. Furthermore, we see that the following species have the highest value of A in gas phase: G-FR5>GB>G2B>G-1F>-G-F>G-C>G-OH>G-COOH>Gi while in water phase the majority have a high value, but those with the highest value are GB>G2B>G-FR5>G-1F>G-C>G-OH>G-F>G-COOH. In this case, the systems that can more readily accept one electron are those doped with B, some models of fluorographene, and some graphene oxide models (with -OH groups). In short, looking at the values of the previous descriptors, one can see that they will more readily accept an electron than donate it, especially, in the water phase, see Figures 3(a), 4(a), Tables S2, and S3. This effect is, possibly, due to the hydrogen capping at the edges. In contrast, the chemical hardness and softness display the same trend as I. On the other hand, the systems with the larger values of I also show a considerable value of η; this means that the systems that have difficulties to donate one electron are because they are hard.
On the other hand, we see a similar trend in ω- and ω+ indexes. That is to say, systems that can more easily donate electron charge compared to pristine G, are G-FR5>GB>G2B>G-1F>G-F>G-C>G-OH>G-COOH>Gi in gas phase and water phase are G2B>G-A>GB>G2P>G-1F>G-C>G-F>G2N>GP>G-COOH> GN. Similarly, the systems that more easily accept electron charges are G-FR5>GB>G2B>G-1F>G-F>G-C>G-OH>G-COOH in the gas phase and, water phase are G2B>G-A>GB>G2P>G-1F>G-C>G-F>G-OH>G2N. In Figures 3(b), 4(b), Tables S2, and S3, one can note that the energy for the donating process has the highest value than that corresponding to the acceptance of electron charge. The last reflects that the functionalized and doped systems can more readily accept electron charge than G (models with the highest value in ω+), in the water phase. Similar results were shown by D. Cortés-Arriagada and B. Saha et. al. for GB, GN, GB, G-OH and G-COOH [20,21].
The energy gap value indicates if a molecule is hard or soft, as the Hard-Soft Acid-Base (HSAB) principle proposed by Pearson states [40]. Therefore, a large value of the gap denotes a hard molecule and the contrary for a small gap. Then, the gap of G (Figures 3(d) and 4(d)) shows that G is a hard acid system in the gas and water phase so that it can react with a hard basis. Our results suggest that the chemical modification made in graphene makes it a softer system, most systems behave as soft acids such as GP>G2P>G-A>GN>G2N>G-HR5>G-1H>G-F>G-COOH>G-C>G-OH in gas phase and G-A>G2P>GP>GB>G2B>G-HR5>G-1H>G-F>G-COOH>G-C>G-HR1>G-OH in water phase. In general, the energy gap of G is reduced with its chemical modifications, especially when doped with a P atom or when functionalized with -OH group, -COOH group and hydrogen atoms.
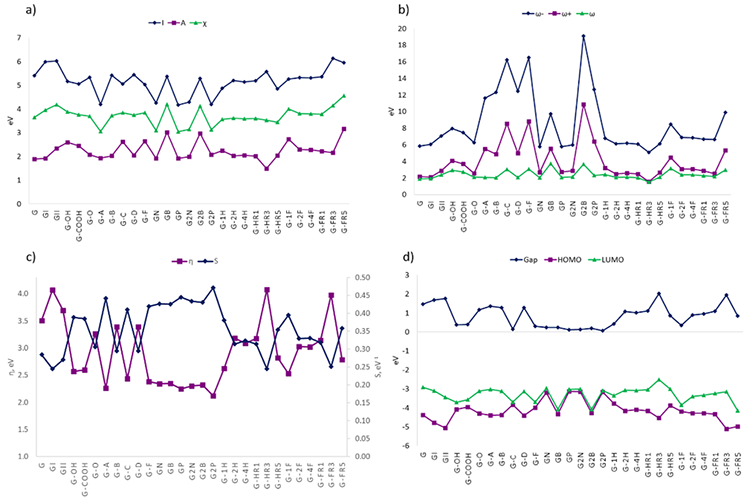
Fig. 3
Gas-phase global descriptors of graphene derivatives at M06-L/6-31G(d) level of theory. In (a) I, A and χ values; (b) ω, ω+and ω-; (c) η and S and (d) Gap, HOMO, and LUMO.
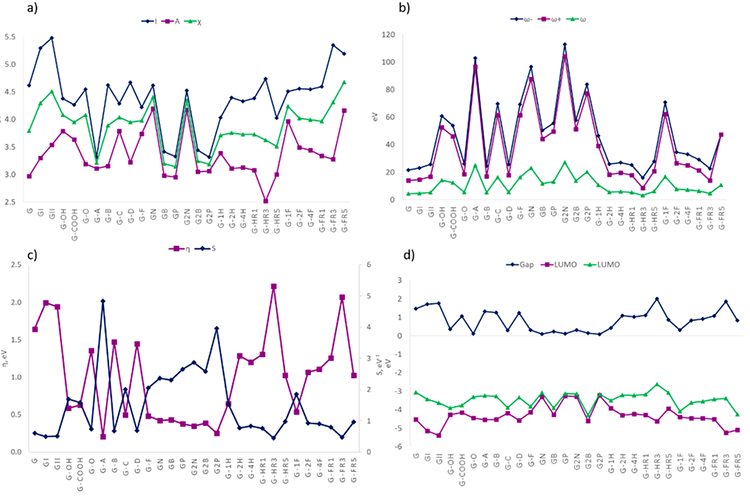
Fig. 4
Water-phase global descriptors of graphene derivatives at M06-L/6-31G(d)/PCM level of theory. In (a) I, A and χ values; (b) ω, ω+and ω-; (c) η and S and (d) Gap, HOMO, and LUMO.
Finally, the Gi and Gii systems cannot be compared against the other chemical modifications. Nevertheless, they can be compared to the pristine G. Gi and Gii show to have a larger affinity to accept one electron and generally electron charge than G. On the other hand, they are harder. Their energy gap is in the semiconducting range so that they may be used in several applications, i.e., sensors. Since they increase their energy gap, they behave better as hard acids so, they should react more readily with hard bases. The previous ones can suffer chemical modifications that would increase the bandgap; some have been discussed in previous works [41,42].
Local descriptors
In the preceding section, we analyzed the changes in global reactivity of the chemically modified G. We analyze the C sites that are closer to the doping and functionalizing groups to avoid the border effect. In this section, the molecular electrostatic potential map (MEP) will be used as a local descriptor. Zones painted with red color corresponds to sites with the most substantial negative charge (more electron density), and the ones with blue color correspond to sites that have a positive charge (less electron density). Finally, we also computed local softness and condensed fukui functions using eqs 9-12 and HOMO and LUMO orbitals as a frozen core approximation.
In Fig. 5, we can note that the C atoms in G
have the most significant values of electron density (red color) so they can be
acceptors for electrophile molecules. In contrast, the border has less (blue color),
so there would be easier acceptance of nucleophilic units. On the other hand, in Fig
S6, we can see that carbon atoms in G have larger HOMO than LUMO values, so the
indicated carbons will be susceptible to interact with electrophile molecules; this
agrees with MEP values. Furthermore, we have the condensed fukui functions and local
softness, in general, these point to the same atoms that the previous HOMO map
shows. The carbon C16, see Fig 2, is more
reactive than the other C atoms in most systems. If taken as reference, then we
compare the changes in fukui values and local softness values in the different
systems chemically modified. One can see in Table
1 that in G, C16 has a large value for 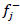 and
and 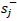 , so that C16 can be a good site for acceptance of electrophile
molecules.
, so that C16 can be a good site for acceptance of electrophile
molecules.
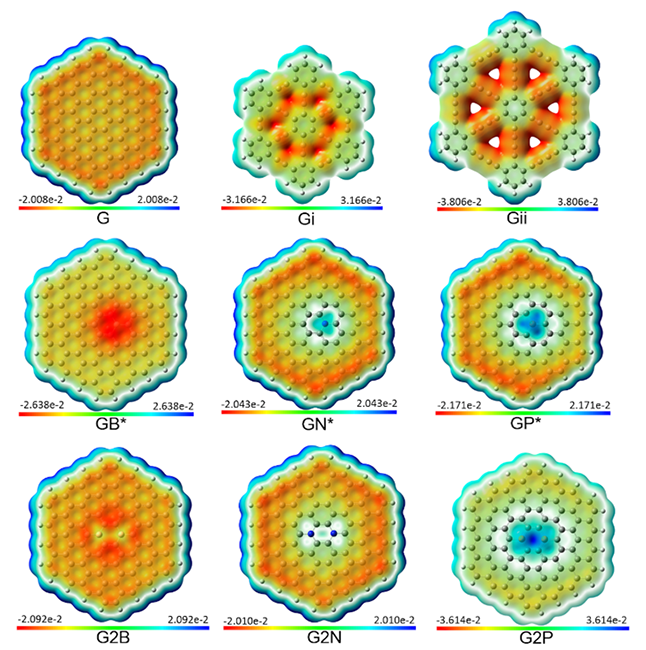
Fig. 5
Molecular electrostatic potential map (MEP) surfaces for graphene, graphyne, graphdiyne, and doped graphene at M06-L/6-31G(d) level of theory. Isosurface mapped for isovalue of 0.0004 u.a.
Condensed fukui function and local softness (in eV-1) of graphene derivatives at the M06-L/6-31G(d) level of theory.
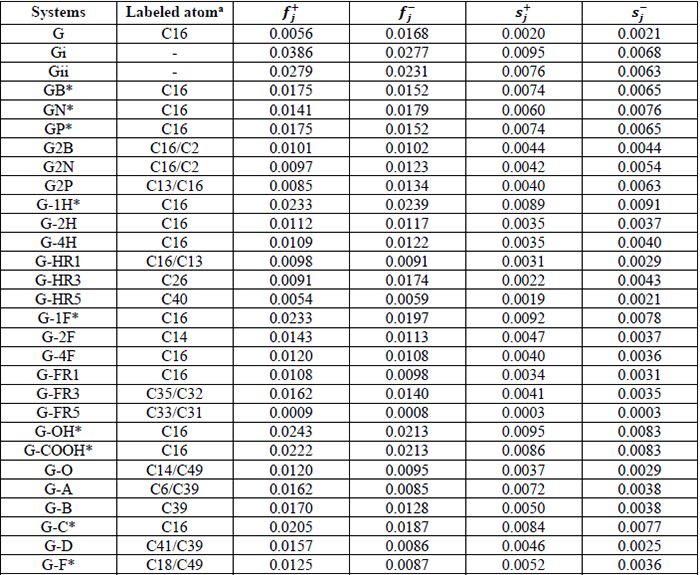
With the chemical modifications made, one can see how the electron density changes throughout the entire system. For example, in GB, G2B, graphene oxide systems, and fluorographene systems (Figures 5-7), one can see an increase in the electron density at the sites where the modification was made, which increases their ability to interact with electrophilic molecules and with nucleophilic molecules (carbon atoms with low electron density). G-F and G-FR5 have more significant changes in their electron density distribution, as one can see in their MEPs. Whereas, the GN, GP, G2N, G2P, and graphane systems show that these chemical modifications cause a lower value of electron density in the modified site so they may better interact with electrophilic molecules. The behavior observed in doped systems GB, GP, and GN was expected according to the electronic structure of P, N and B and is in agreement with works of D. Cortés Arriagada and B. Saha et. al.; despite our larger models [20,21]. According to the MEP values in the graphane modified systems, they do not change their charge distribution significantly as compared to pristine G, so the interaction with electrophilic molecules should be weak. Finally, in Gi and Gii models, the acetylenic linkages have more electron density helping their ability to interact with electrophilic molecules.
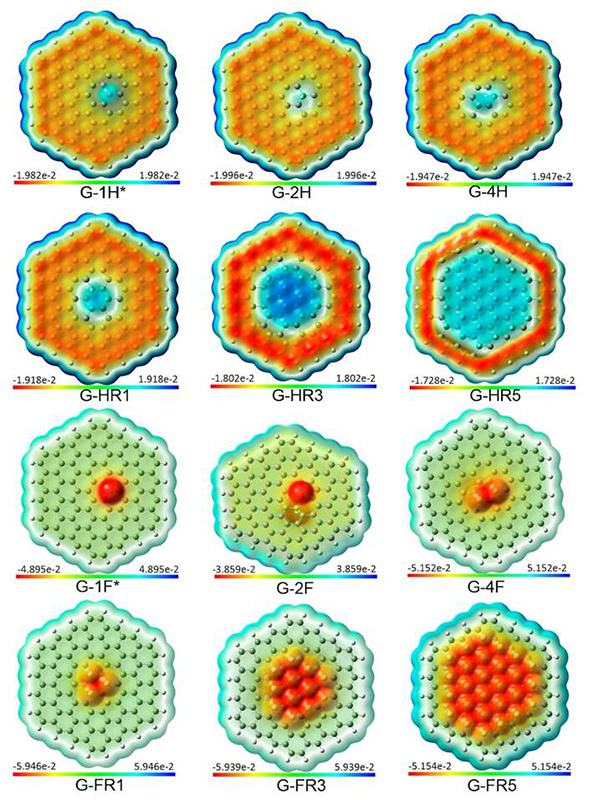
Fig. 6
Molecular electrostatic potential map (MEP) surfaces for graphane and fluorographene in different compositions. Isosurface mapped for isovalue of 0.0004 u.a.
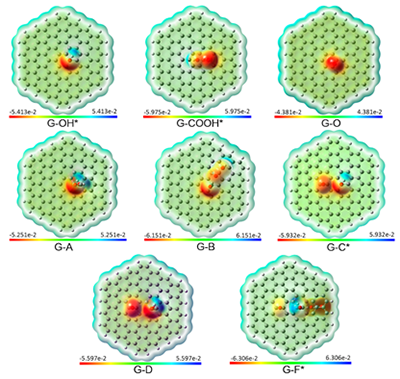
Fig. 7
Molecular electrostatic potential map (MEP) surfaces for different graphene oxide models at M06-L/6-31G(d) level of theory. Isosurface mapped for isovalue of 0.0004 u.a.
On the other hand, carbon sites as C16 have higher values of 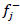 and
and 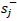 in G-1H>GN>G2P>G2N>G-HR3>G-2H as compared to pristine G.
For
in G-1H>GN>G2P>G2N>G-HR3>G-2H as compared to pristine G.
For 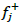 and
and 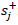 ,
Gi>G-OH>G-1F>G-COOH>G-C>Gii>GB>GP>G-A>G-F>G-B>G-2F>G-D>G-FR3>G-4F>G-O>G-FR1>G-HR,
see Table 1. This result means that the
interaction with electrophilic or nucleophile molecules will be easier for these
derived systems than in pristine G.
,
Gi>G-OH>G-1F>G-COOH>G-C>Gii>GB>GP>G-A>G-F>G-B>G-2F>G-D>G-FR3>G-4F>G-O>G-FR1>G-HR,
see Table 1. This result means that the
interaction with electrophilic or nucleophile molecules will be easier for these
derived systems than in pristine G.
Conclusion
An extensive study was carried out to understand and describe changes in reactivity due to doping and functionalization in graphene systems and how this modifies their ability for possible interactions with other molecules such as drugs.
We are aware that some features of our level of theory and structural or computational models chosen, due to the complexity of the studied systems and computational cost, may cause that some computed properties are less accurate than others. This is the case for instance with our choice for the PCM solvent model. For these solvent models, the errors in the solvation energies are larger in the case of anions in comparison to cations. This may be improved by taking into account water molecules explicitly, although the increase in computational cost is beyond the scope of this work. Our solvent model, although simpler and less accurate, provides insight in the trends of the changes in reactivity of our sample of systems in water as compared to gas phase.
We analyzed the structural characteristics of all systems, and it was found that sp3 hybridization is present in the closer doped/functionalized C-C distances, showing pyramidalized bonds. The antiperiplanar conformation is preferred for the attached atoms. Consequently, doping or functionalizing G changes its structure and some properties. The latter has been correlated with the computed values of the conceptual DFT reactivity indexes. For example, the low values of I, and ω- shows that the systems doped with P or B atoms, the pristine graphane, and graphene with an -OH or -COOH group as well as the systems with higher values of A and ω+ such as complete fluorographene and graphene doped with B atoms can easily allow the adsorption of different species into them.
Furthermore, these systems can more easily accept electron charge than pristine G, improving its possible chemisorption. With the computed local descriptor indexes, one can see the specific sites where the external molecules may have a good interaction in the graphene systems. With the local descriptors indexes, we see that due to the increase of the electron density at the sites where the modification was made, this increases their ability to interact with electrophilic molecules and with nucleophilic molecules, especially for the complete graphene oxide model, graphene with -COOH or -OH group, complete fluorographene, and G doped with a P atom. Also, Gi and Gii are found to be better to accept electrophiles, and this could be enhanced with chemical modifications as made on pristine G. Then, these systems could improve their potential to be used for drug delivery.
Chemical modifications on pristine G, make it a softer molecule. According to the HSAB principle, these systems could interact more easily with electrophiles or nucleophiles. In consequence, these derivatives of G are amenable to the customization of their electronic properties through controlled functionalization, as systematically discussed in this paper. Our chosen finite model is not intended to represent the pristine (extended) graphene system but rather the (finite) graphene flake. However, at carbons far from the border one gets the idea of the extended system situation, i.e. it could be considered that at R3 atoms, Fig. 2, the chemical environment is similar to pristine extended graphene; R3 atoms have no edge effect. Then, with the analysis of the local descriptors of reactivity, one can get an idea of the behavior that graphene has when it is chemically modified. But certainly, our main goal is to model the flakes, which experimentally are very promising for chemical applications. Indeed, the flake model has a well-defined gap whereas graphene is gapless; as can be seen from Fig. S6, in our finite model for graphene and derivatives, the HOMO and LUMO have strong contributions from the capping region that would not be active in the reactivity of pristine (extended) graphene but certainly are expected in the finite, capped flakes; this situation is also present in the other derived systems and are promising for further chemical functionalization sites.Therefore, one can expect the possibility of fabricating G derivatives suitable to be used in several applications such as in biomedical applications, drug transport and biosensors.
Acknowledgments
Guanajuato National Laboratory (CONACYT 1237332) is acknowledged for supercomputing resources. BM acknowledges support from CONACYT for a Ph.D. scholarship (580068/296892). JR gratefully acknowledges funding from University of Guanajuato (DAIP-Convocatoria Institucional de Investigación Científica 2018, Project No. 268.
References
1. Falcao, E. H. L.; Wudl, F. J. Chem. Technol. Biotechnol. 2007, 82, 524-531. https://doi.org/10.1002/jctb.1693
2. Yola, M. L. Curr. Anal. Chem. 2019, 15, 159-165. https://doi.org/10.2174/1573411014666180320111246
3. Gu, H.; Tang, H.; Xiong, P.; Zhou, Z. Nanomaterials 2019, 9, 130. https://doi.org/10.3390/nano9010130
4. Kang, J.; Wei, Z.; Li, J. ACS Appl. Mater. Interfaces 2019, 11, 2692-2706. https://doi.org/10.1021/acsami.8b03338
5. Yeo, J.; Jung, G. S.; Martín-Martínez, F. J.; Beem, J.; Qin, Z.; Buehler, M. J. Adv. Mater. 2019, 1805665, 1-24. https://doi.org/10.1002/adma.201805665
6. Novoselov, K. S.; Geim, A. K.; Morozov, S. V; Jiang, D.; Zhang, Y.; Dubonos, S. V; Grigorieva, I. V; Firsov, A. A. Science. 2004, 306, 666-669. https://doi.org/10.1126/science.1102896
7. Geim, A. K.; Novoselov, K. S. Nat. Mater. 2007, 6, 183-191. https://doi.org/10.1038/nmat1849
8. Baughman, R. H.; Eckhardt, H.; Kertesz, M. J. Chem. Phys. 1987, 87, 6687-6699. https://doi.org/10.1063/1.453405
9. Cranford, S. W.; Brommer, D. B.; Buehler, M. J. Nanoscale 2012, 4, 7797-7809. https://doi.org/10.1039/C2NR31644G
10. Peng, Q.; Dearden, A. K.; Crean, J.; Han, L.; Liu, S.; Wen, X.; De, S. Nanotechnol. Sci. Appl. 2014, 7, 1-29. https://doi.org/10.2147/NSA.S40324
11. Zhang, W.; Wu, L.; Li, Z.; Liu, Y. RSC Adv. 2015, 5, 49521-49533. https://doi.org/10.1039/C5RA05051K
12. Shin, D.-W.; Kim, T. S.; Yoo, J.-B. Mater. Res. Bull. 2016, 82, 71-75. https://doi.org/10.1016/j.materresbull.2016.02.009
13. Yadav, R.; Dixit, C. K. J. Sci. Adv. Mater. Devices 2017, 2, 141-149. https://doi.org/10.1016/j.jsamd.2017.05.007
14. Agnoli, S.; Favaro, M. J. Mater. Chem. A 2016, 4, 5002-5025. https://doi.org/10.1039/C5TA10599D.
15. Chronopoulos, D. D.; Bakandritsos, A.; Pykal, M.; Zbořil, R.; Otyepka, M. Appl. Mater. today 2017, 9, 60-70. https://doi.org/10.1016/j.apmt.2017.05.004
16. Singh, D. P.; Herrera, C. E.; Singh, B.; Singh, S.; Singh, R. K.; Kumar, R. Mater. Sci. Eng. C 2018, 86, 173-197. https://doi.org/10.1016/j.msec.2018.01.004
17. Lee, J.-U.; Yoon, D.; Cheong, H. Nano Lett. 2012, 12, 4444-4448. https://doi.org/10.1021/nl301073q.
18. Luo, B.; Liu, S.; Zhi, L. Small 2012, 8, 630-646. https://doi.org/10.1002/smll.201101396
19. Geerlings, P.; De Proft, F.; Langenaeker, W. Chem. Rev. 2003, 103, 1793-1874. https://doi.org/10.1021/cr990029p
20. Cortés Arriagada, D. J. Mol. Model. 2013, 19, 919-930. https://doi.org/10.1007/s00894-012-1642-6
21. Saha, B.; Bhattacharyya, P. K. RSC Adv. 2016, 6, 79768-79780. https://doi.org/10.1039/C6RA15016K
22. SreeHarsha, N.; Maheshwari, R.; Al-Dhubiab, B.E.; Tekade, M.; Sharma, M.C.; Venugopala, K.N.; Tekade, R.K.; Alzahrani, A.M. Int. J. Nanomedicine. 2019,14, 7419-7429. doi:10.2147/IJN.S211224
23. Janak, J. F. Phys. Rev. B 1978, 18, 7165-7168. https://doi.org/10.1103/PhysRevB.18.7165
24. Casida, M. E. Phys. Rev. B 1999, 59, 4694-4698. https://doi.org/10.1103/PhysRevB.59.4694
25. Parr, R. G.; Pearson, R. G. J. Am. Chem. Soc. 1983, 105, 7512-7516. https://doi.org/10.1021/ja00364a005
26. Parr, R. G.; Yang, W. J. Am. Chem. Soc. 1984, 106, 4049-4050. https://doi.org/10.1021/ja00326a036
27. Gázquez, J. L.; Cedillo, A.; Vela, A. J. Phys. Chem. A 2007, 111, 1966-1970. https://doi.org/10.1021/jp065459f
28. Yang, W.; Mortier, W. J. J. Am. Chem. Soc. 1986, 108, 5708-5711. https://doi.org/10.1021/ja00279a008
29. Yang, W.; Parr, R. G. Proc. Natl. Acad. Sci. 1985, 82, 6723-6726. https://doi.org/10.1073/pnas.82.20.6723
30. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; et al. Gaussian 09. Revision C.01, Gaussian, Inc, Wallingford CT. Gaussian, Inc.: Wallingford CT 2010.
31. Zhao, Y.; Truhlar, D. G. J. Chem. Phys. 2006, 125, 194101. https://doi.org/10.1063/1.237099
32. Francl, M. M.; Pietro, W. J.; Hehre, W. J.; Binkley, J. S.; Gordon, M. S.; DeFrees, D. J.; Pople, J. A. J. Chem. Phys. 1982, 77, 3654-3665. https://doi.org/10.1063/1.444267
33. Hirshfeld, F. L. Theor. Chim. Acta 1977, 44, 129-138. https://doi.org/10.1007/BF00549096.
34. Miertuš, S.; Scrocco, E.; Tomasi, J. Chem. Phys. 1981, 55, 117-129. https://doi.org/10.1016/0301-0104(81)85090-2
35. Barnard, A. S.; Snook, I. K. J. Chem. Phys. 2008, 128, 94707. https://doi.org/10.1063/1.2841366
36. Silva, A. M.; Pires, M. S.; Freire, V. N.; Albuquerque, E. L.; Azevedo, D. L.; Caetano, E. W. S. J. Phys. Chem. C 2010, 114, 17472-17485. https://doi.org/10.1021/jp105728p
37. Kuc, A.; Heine, T.; Seifert, G. Phys. Rev. B 2010, 81, 85430. https://doi.org/10.1103/PhysRevB.81.085430
38. Deng, J.-P.; Chen, W.-H.; Chiu, S.-P.; Lin, C.-H.; Wang, B.-C. Molecules 2014, 19, 2361-2373. https://doi.org/10.3390/molecules19022361
39. Puigdollers, A. R.; Alonso, G.; Gamallo, P. Carbon N. Y. 2016, 96, 879-887. https://doi.org/10.1016/j.carbon.2015.10.043
40. Pearson, R. G. Acc. Chem. Res. 1993, 26, 250-255. https://doi.org/10.1021/ar00029a004.
41. Peyghan, A. A.; Rastegar, S. F.; Hadipour, N. L. Phys. Lett. A 2014, 378, 2184-2190. https://doi.org/10.1016/j.physleta.2014.05.016
42. Ketabi, N.; Tolhurst, T. M.; Leedahl, B.; Liu, H.; Li, Y.; Moewes, A. Carbon N. Y. 2017, 123, 1-6. https://doi.org/10.1016/j.carbon.2017.07.037
Author notes
*Corresponding author: Juvencio Robles, email: roblesj@ugto.mx

 cygnusmind
cygnusmind