Journal of the Mexican Chemical Society, vol. 63, no. 2, 2019
Sociedad Química de México A.C.
Benjamín Cortes-Sánchez
Universidad Nacional Autónoma de México, Mexico
David Cruz-García
Universidad Nacional Autónoma de México, Mexico
Milton Medeiros *
Universidad Nacional Autónoma de México, Mexico
Date received: 29 January 2019
Date accepted: 17 April 2019
Funding
Funding source: Facultad de Química-UNAM PAIP
Contract number: 5000-9017
Funding
Funding source: CONACyT
Contract number: 429376
Abstract.: The Cubic Two-State equation of state was employed to correlate the measured mutual solubilities of water and 23 chlorinated hydrocarbons (CHCs). Following the scheme framework laid out by Medeiros and Brindis-Flores, a nonquadratic Kabadi-Danner type mixing rule is used, where the water-water dispersive parameter is corrected due to the presence of a hydrophobic solute. The model’s three parameters were adjusted to correlate experimental binary liquid-liquid equilibrium data to relatively high accuracy. The observed minimum in CHC solubility in water near ambient conditions is reproduced reliably. Overall deviations from experimental data were 7.8% for CHC solubility in the aqueous phase and 13% for water solubility in the organic phase.
Keywords: Mutual Solubilities, Chlorinated Hydrocarbons, Liquid-Liquid Equilibrium, Equation of State.
Resumen.: La ecuación de estado Cubic Two-State fue empleada para correlacionar las solubilidades mutuas experimentales de sistemas binarios de agua y 23 hidrocarburos clorados (CHC’s). Siguiendo el precedente establecido por Medeiros y Brindis-Flores, se utilizó una regla de mezclado no cuadrática tipo Kabadi-Danner, donde el parámetro dispersivo de la interacción agua-agua es corregido debido a la presencia de solutos hidrofóbicos. Los tres parámetros del modelo se ajustaron de forma de correlacionar los datos experimentales con exactitud relativamente alta. El mínimo de solubilidad de CHC en agua observado en condiciones próximas al ambiente se reprodujo consistentemente. La desviación de los datos calculados respecto a los experimentales fue 7.8% para la solubilidad de CHC en la fase acuosa y 13% para la solubilidad de agua en la fase orgánica.
Palabras clave: Solubilidades Mutuas, Hidrocarburos Clorados, Equilibrio Líquido-Líquido, Ecuación de Estado.
Introduction
The presence of water in organic process streams has long been an important concern in industrial processes, where evaluating the water content of an oil sample or organic process stream is a priority, be it in the design and optimization phase of a plant’s life, or in the maintenance of it, as water can damage equipment due to corrosion, two phase flow or blockages due to sediment deposits.
Liquid-liquid equilibria (LLE) of chlorohydrocarbons (CHCs) and water occur frequently in industrial and environmental contexts. These systems are present in a wide variety of chemical processes, such as the PVC industry; determining the solubility of water in the organic phase is important for its separation from organic streams. CHCs are also an environmental concern, they have been identified as major groundwater pollutants [1] and have been labeled as persistent organic pollutants (POP) by the 2004 Stockholm Convention of 2004 [2], which restricted their use. As such, it is important to study the solubility of these substances in water for the potential treatment and remediation of contaminated aquifers and reduce their damage to ecosystems.
Studies of mutual solubilities of water and non-halogenated hydrocarbons have been undertaken by several groups, via equations of state (EoS), models of solution, and empirical correlations, among other methods. A summary of these approaches is presented by Oliveira et al. [3]. The EoS approach easily correlates the solubility of water in hydrocarbons using a temperature-independent binary interaction parameter. However, a challenge arises when calculating the hydrocarbon solubility in water, due to the inability of the cubic EoS with conventional mixing rules to account for the hydrophobic hydration effect; thus, the resulting correlation with experimental results is poor, and it fails to predict the observed minimum solubility near ambient conditions [3,4]. To overcome this deficiency, unconventional mixing rules are required. Kabadi and Danner [5], Michel et al. [6] and Nasrifar and Moshfeghian [7,8] proposed nonquadratic mixing rules for the dispersive parameter of the Soave-Redlich-Kwong (SRK), Peng-Robinson (PR) and other cubic EoS. The main idea is to correct the water-water interaction due to hydrophobic hydration effects caused by the presence of the organic solute. Our group applied the idea of Kabadi and Danner [5] to the Cubic Plus-Association (CPA) [9] and to the Cubic Two-State (CTS) EoS [10]. The proposed model reproduced the observed minimum in HC solubility reliably and presented a marked relationship with the chemical family and structure of HC heavier than butane [10].
On the other hand, thermodynamic equilibrium studies of water-CHC systems are scarce. Senol [11] studied the LLE of water-carboxylic acid-chloroform systems using a solvation energy based on a UNIFAC model, with the intent of extracting carboxylic acids from water using chloroform. Sengupta, et. al [12] modeled the extraction of chlorinated hydrocarbons from water with supercritical CO2, using the Carnahan-Starling-DeSantis-Redlich-Kwong (CSDRK) EoS, a hard-sphere perturbation model modification to the Redlich-Kwong EoS. In that work, mutual solubilities for three binary water-CHC systems were calculated at two temperatures. The binary interaction parameter for these systems was obtained from ternary data modeling, with one parameter for each temperature. This study does not present a predictive model for water-chlorohydrocarbon mutual solubility calculations.
Predictive mutual solubility studies of water and CHCs from cubic EOSs with unconventional mixing rules are yet to be carried out. Similar challenges to those faced by water-HC calculations arise in the modeling of water-CHC systems, such as the prediction of the observed minimum in solubility near ambient conditions. Also, the introduction of a voluminous substituent, such as chlorine, makes the solubility of chloroalkanes in water orders of magnitude higher than that of aliphatic hydrocarbons. Experimental data availability brings new challenges to the table.
The main objective of this work is to extend the predictive scheme model developed by Medeiros and Brindis-Flores [10] for water-HC mutual solubility determination to cover water-CHC mixtures. We also employed the CTS EoS coupled to a non-quadratic mixing rule, which corrects the dispersive parameter where the water-water interaction is modified due to the presence of hydrophobic solutes. Mutual solubility data of 23 chlorinated alkanes were correlated in this work, from chloromethanes to chloropentanes.
This paper is structured in four major sections: First, a brief description of the CTS EoS is given, where the parameters and descriptions of the mixing rules used are explained. Afterwards, we present the procedures used to fit the model to experimental data and the obtained mixing rules parameters are discussed. Next, results and model predictions are presented, and finally, conclusions and closing remarks are given.
The CTS equation of state
The CTS (Cubic Two-State) equation is derived from a combination of two contributions to the Helmholtz energy of a system: a physical part given by the Soave-Redlich-Kwong EoS and a molecular associative term obtained from the Two-State Association model [13]. Its pressure-explicit form is:
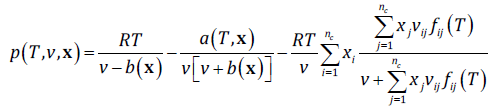 (1)
(1)Where, p is the system pressure, R is the gas constant, v is the molar volume, x is the vector of mole fractions, b(x) is the mixture co-volume, a(T,x) is the mixture dispersive parameter, n c is the number of components in the mixture, x i refers to the molar fraction of the component i, v ij is the characteristic association volume for the pair i-j, and f ij (T) is the Mayer function:
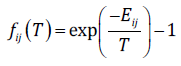 (2)
(2)In Eq. 2, E ij is the energy of association for the pair i-j. The mixture co-volume is given by the conventional van der Waals mixing rule:
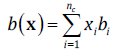 (3)
(3)For the mixture dispersive parameter, the rule suggested by Medeiros and Brindis-Flores [10] is used, where, following Kabadi and Danner’s proposal [5], a correction function φ(T, x) is introduced to correct the water-water dispersive a 11 due the presence of hydrophobic solutes. The rule has the following form:
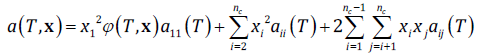 (4)
(4)The subscript 1 refers to water for the remainder of this work. For pure substances, a ii has the form suggested by Soave:
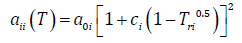 (5)
(5)where, T ri is the reduced temperature for the substance i, T ri = T/T ci , and T ci is the critical temperature of the substance i. In Eqs. 3 and 5 for self-associating compounds, a 0i , b i and c i are adjustable pure parameters. The cross a ij is given by the geometric mean combining rule:
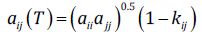 (6)
(6)where k ij is an adjustable binary interaction parameter. The correction function φ(T, x) has the form suggested by Medeiros and Brindis-Flores [10]:
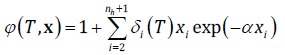 (7)
(7)where n h is the number of hydrophobic solutes, α = 10, and δ i is given by:
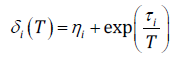 (8)
(8)where η i and τ i are adjustable parameters related to the hydrophobic solute i. The development and testing of this expression can be found in Medeiros and Brindis-Flores’ work [10]. It is important to note that, in Eq. 7, the entropic effects induced by the solutes are independent. The mixing rule has been tested for compliance with the Gibbs-Duhem condition, and it is shown that it does not violate it [10]. The CTS expression for fugacity coefficient determination is:
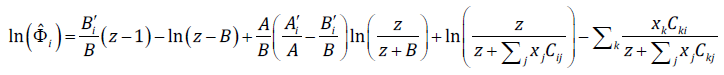 (9)
(9)
where:
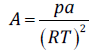 (10)
(10)
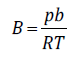 (11)
(11)
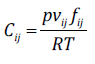 (12)
(12)
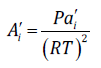 (13)
(13)
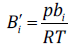 (14)
(14)and z is the compressibility factor of the mixture. For water-CHC systems, the compressibility-explicit form of the CTS EOS is a fourth-degree polynomial. In Eq. 13, the derivative of the dispersion parameter for water, is given by:
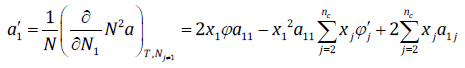 (15)
(15)and for hydrophobic CHCs:
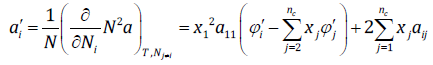 (16)
(16)where,
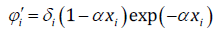 (17)
(17)We assumed that CHCs are non-self-associating substances and do not form association complexes with water. As such, the values of the cross-association parameters E ij and v ij are zero, and, for CHCs, the SRK parameters are calculated using the corresponding state expressions
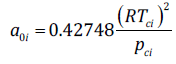 (18)
(18)
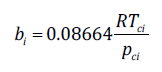 (19)
(19)
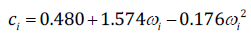 (20)
(20)where, T ci and p ci are the critical temperature and pressure, respectively, and ω i is Pitzer’s acentric factor. Values for T ci , p ci and ω i were taken from the Aspen Plus V8.8 database. For self-associating substances, such as water, the physical and association parameters were taken from Medeiros and Téllez-Arredondo [13], who obtained them by fitting the CTS model to measured pressures and densities at saturation conditions. They also showed that the parameters a 0i and b i have a similar interpretation to the van der Waals’ parameters for non-polar molecules, with a 0i being related to intermolecular dispersion energy and b i to the molecular volume. Furthermore, the CTS association energy E ij , is very similar to other association models’ parameters, such as SAFT [14] and CPA [15] and is compatible with experimental hydrogen bond energy. Furthermore, characteristic association volumes v ij are related to association site availability. Molecules with easily accessible association sites have a higher v ij . The complete development of the model from statistical thermodynamics can be seen elsewhere [13].
The CTS EoS can be transformed into a compressibility polynomial that can be solved by robust methods such as Laguerre’s, which was used in this work. The CTS equation has lower numerical complexity than other association models, such as CPA and SAFT, due to its lack of association schemes. Therefore, its processing cost is much lower, although it does require a higher computing time compared to traditional cubic equations like Peng-Robinson and SRK.
Parameter regression
For correlating mutual solubilities, the model has three adjustable parameters, k ij , η i , and τ i . These parameters were obtained by fitting the model to experimental data for 23 CHCs taken from IUPAC-NIST compilations and from the literature [16-41]. The objective function to be minimized was:
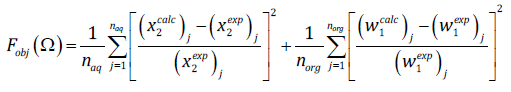 (21)
(21)where ω is the vector of adjustable parameters, x 2 refers to the chlorohydrocarbon solubility in the aqueous phase, w 1 is the water solubility in the organic phase, and n aq and n org are the number of measured data points for the aqueous and organic phases, respectively. We used the conjugate gradient method for function minimization. Following IUPAC criteria for water-HC systems [42], it was aimed, for calculated mutual solubilities, to not exceed 30% deviation from experimental results. The average absolute deviation (AAD %) was used to gauge these deviations. It is defined by:
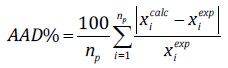 (22)
(22)The superscripts calc and exp refer to the solubilities calculated by the model and measured, respectively, and n p is the number of experimental points. Liquid-liquid flash calculations were performed at a given temperature and pressure for each water-CHC pair, leaving only material equilibrium of the system to be solved. The flash equations are:
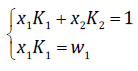 (23)
(23)where x 1 and x 2 are the water and CHC fractions in the aqueous phase, w 1 refers to the water fraction in the organic phase, and:
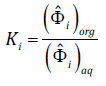 (24)
(24)The system of equation Eq. 23 was solved for x 2 and w 1 using the Levenberg-Marquardt method. To obtain the fugacity coefficients, first, the polynomial compressibility form of the CTS EoS is solved, and the liquid phase z corresponds to the lowest positive non-zero root. In order to get better convergence, correlations of measured mutual solubilities, for each water-CHC pair, were performed in three steps: (i) from water solubilities in the organic phase, regressions were carried out with ω=k ij using the van der Waals mixing and combining rules for the dispersive parameter a. At this step, no correction function was introduced, and a preliminary value for k ij is obtained; (ii) a second regression was performed from data for both phases, with ω=(η i ,τ i ) and with the previously obtained value for k ij ; and (iii) finally, a full calculation was performed with ω=(k ij ,η i ,τ i ) using the parameters from the previous two steps as guess values. In the cases where data were only available for the aqueous phase, a single regression with ω=(η i ,τ i ) was done, with k ij =0 (see next section). Regressions were performed by increasing the CHC chain length. Initial guess values for η i and τ i were taken from Medeiros and Brindis-Flores’ [10] for the equivalent non-chlorinated compound with the same carbon chain length (e.g., regressed parameters for methane were used as initial guess values for methyl chloride calculations). Afterwards, guess values for compounds with a higher number of chlorine substituents were taken from the previous simplest compound, if available. For example, results for dichloromethane were used as guess values for chloroform and so on.
Results and discussion
Table 1 shows the adjusted values of k ij , η i and τ i for each water-CHC pair and the absolute average deviations of our model from experimental measurements. The comparisons among calculated and experimental data are plotted in figures 1 and 2, for the aqueous and oil phases respectively. For several water-CHC pairs, experimental data present high dispersion, especially in the organic phase, as shown in Fig. 3 for CH2Cl2, CHCl3, and CCl4. Due to limited measured data availability, a systematic selection of data was not performed, although points that clearly deviate from the general trends were removed from fittings. As a general rule, the regressions yielded higher AAD% than those observed in our group’s previous work with aliphatic HCs [10], where recommended data were widely available. Additionally, absolute average deviations of LLE calculated with NRTL model parameters in Aspen Plus are also reported in Table 1. While both methods are comparable, CTS requires fewer adjustable constants than NRTL, which needs between 3 and 7 binary parameters to adequately reproduce the LLE. NRTL binary parameters were taken directly from the Aspen Plus database.
Water-CHC adjusted mixing rule parameters, number of NRTL parameters and model deviations from experimental data.
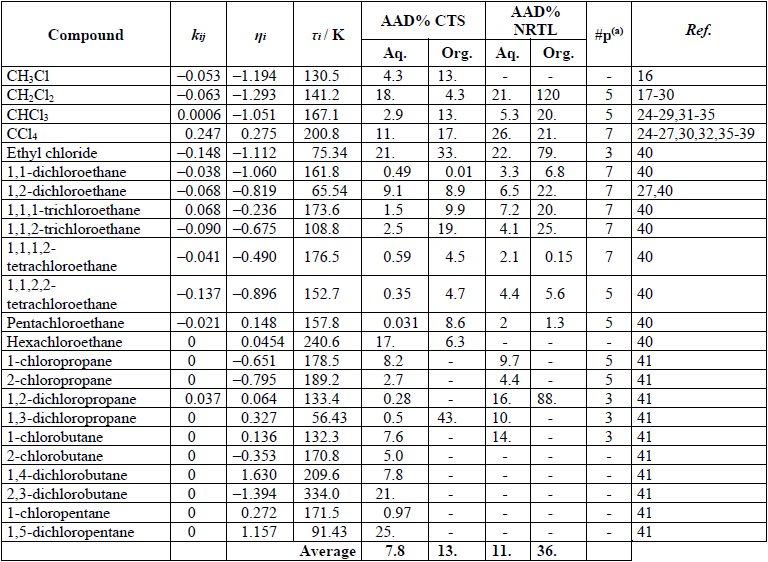
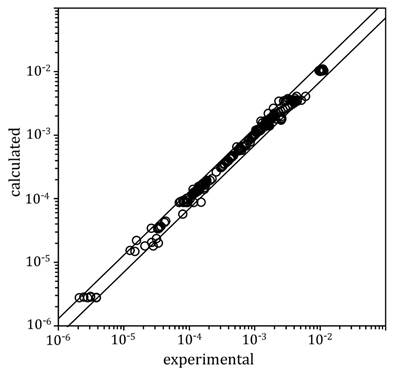
Fig. 1
Calculated and measured solubilities of chlorohydrocarbons in the aqueous phase. Lines represent the ±30% AAD region.
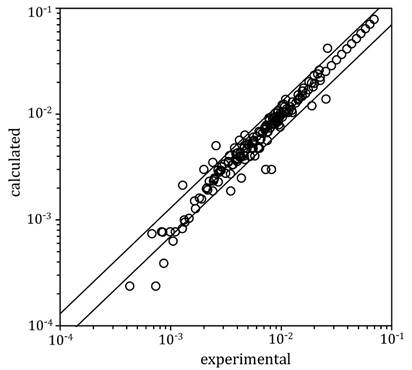
Fig. 2
Calculated and measured solubilities of water in the chlorohydrocarbon rich phase. Lines represent the ±30% AAD region.
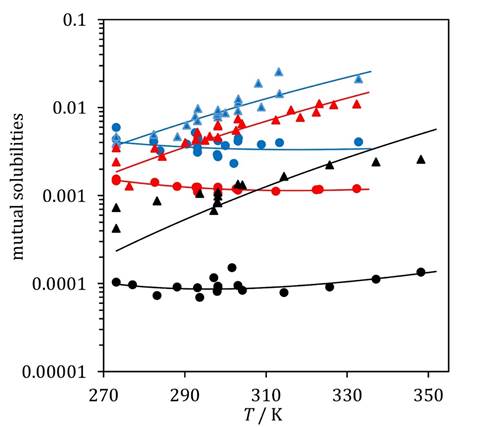
Fig. 3
Mutual solubilities of water and carbon tetrachloride (black), chloroform (red) and dichloromethane (blue). Circles: experimental solubilities of chloromethanes in the aqueous phase [17,39]. Triangles: experimental solubilities of water in the organic phase [17-39]. Lines: model calculated solubilities.
Apart from three water-CHC pairs (CCl4, chloroethane and 1,1,2,2-tetrachloroethane), the absolute value of k ij was always lower than 0.1. Across all binary systems, values for k ij obtained from two phase regression did not significantly change in value compared to those resulting from organic phase data regression only. The parameters η i and τ i are mostly responsible for fitting the aqueous phase data, while the impact of k ij largely lies on correlating organic phase data. Hence, when no experimental data for the organic phase were available, k ij was set to zero.
In contrast to our group’s observation [10] for water-HC, the calculated values for the three parameters k ij , η i and τ i follow no discernible tendencies with the co-volume of the respective CHC. Furthermore, unlike the previous work on water-HC systems [10], for some CHCs, the correlated solubilities in aqueous phase versus temperature curves do not present the same slope as the experimental data, which can be seen for CCl4 in Fig. 3.
As expected, the mixing rule correlated the solubility of hydrocarbons in water accurately. Deviations were small for aqueous phase calculations, as the mixing rule’s correction function accounts for the alteration of water-water interactions by the presence of a hydrophobic solute and, thus, it better describes the water-rich phase than the conventional van der Waals mixing rule. Fig.1 illustrates that most of the calculated points lie within the ±30% deviation region. Liquid-liquid calculations using the obtained parameters were consistently able to predict the observed minimum in aqueous phase solubility. figures 3 and 4 illustrate this for chloromethanes and chloroethanes, respectively. Overall deviation for chlorohydrocarbon solubility in the aqueous phase was 7.8%.
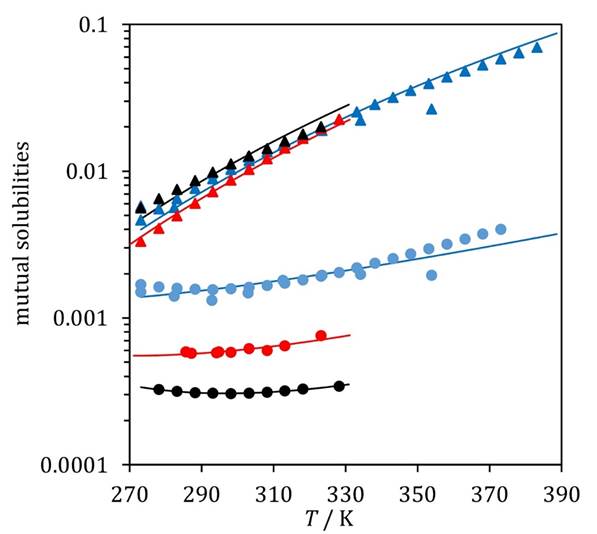
Fig. 4
Mutual solubilities of water and 1,2-dichloroethane (blue), 1,1,2-trichloroethane (red), and 1,1,2,2-tetrachloroethane (black). Circles: experimental solubilities of chloroethanes in the aqueous phase [27,40]. Triangles: experimental solubilities of water in the organic phase [40]. Lines: model calculated solubilities.
Regarding water solubility in the organic phase, higher deviations were obtained than in our group’s work with water-aliphatic HC mixtures [10], where the water solubility is closely correlated with a single binary interaction parameter k ij . The CTS EoS is not able to represent the dipolar and quadrupolar interactions, so the organic phase, unlike in the case of aliphatic hydrocarbons, cannot be well represented with the SRK EoS. Additional calculations were made in order to check possible improvements for water solubility in the organic phase. We hypothesized a cross-association between water and CHCs; however, the correlation did not improve. Moreover, we tested the CPA equation of state in the determination of mutual solubilities of water-chlorohydrocarbon binary mixtures using the modification previously described to the dispersive term. No enhancement was observed compared to the CTS EoS. This supports our idea that the dispersive term of the SRK equation is not able to reproduce water solubility in the chlorinated hydrocarbon phase, i.e., an additional term is required to quantify the polar and quadrupolar interactions of the halogenated hydrocarbon. Fig. 2 illustrates calculated solubilities of water in the organic phase and their deviation from experimental data. Overall deviation for water solubility was 13%. To the best of our knowledge, there are no experimental data of liquid-liquid equilibrium of multicomponent water-CHC’s, so we could not test the model in a predictive way for multicomponent systems.
Conclusions
The mixing rule developed by Medeiros and Brindis-Flores for the CTS EoS was expanded to the correlation of water-CHC systems with the CTS EoS. This mixing rule modifies the water-water dispersive interaction in the presence of hydrophobic solutes. The three parameters were obtained by fitting the model to the available measured mutual solubilities. The model reproduced mutual solubilities in both phases accurately in a wide range of temperatures, with fewer binary parameters than NRTL. Further work is required to account for the observed water solubility deviation from experimental results. The proposed model can easily be extended to other hydrophobic solutes, such as other halogenated hydrocarbon, esters and ethers, as well as multicomponent VLLE systems.
Acknowledgments
We are grateful for funding from Facultad de Química-UNAM PAIP 5000-9017. B.C.S. was supported by CONACyT under a Ph.D. scholarship #429376.
References
1. Schwille, F. The Science of the Total Environment. 1985, 21, 173-185.
2. Stockholm Convention on persistent organic pollutants. 2009, Annexes A-C. 33-51.
3. Oliveira, M. B.; Coutinho, J. A. P.; Queimada, A. J. Fluid Phase Equilib. 2007, 258, 58-66.
4. Economou, I. G.; Tsonopoulos, C. Chem. Eng. Sci. 1997, 52, 511-525.
5. Kabadi, V. N.; Danner, R. P. Ind. Eng. Chem. Process Des. Dev. 1985, 24, 537-541.
6. Michel, S.; Hooper, H. H.; Prausnitz, J. M. Fluid Phase Equilib. 1989, 45, 173-189.
7. Nasrifar, K.; Moshfeghian, M. Fluid Phase Equilib. 2002, 193, 261-275.
8. Reshadi, P.; Nasrifar, K.; Moshfeghian, M. Fluid Phase Equilib. 2011, 302, 179-189.
9. Medeiros, M. Fluid Phase Equilib. 2014, 368, 5-13.
10. Medeiros, M.; Brindis-Flores, C. C. Ind. Eng. Chem. Res. 2017, 56, 2277-2286.
11. Senol, A. Fluid Phase Equilib. 2006, 243, 51-56.
12. Sengupta, S.; Gupta, S.; Dooley, K. M.; Knopf, F. C. The Journal of Supercritical Fluids 1994, 7, 201-209.
13. Medeiros, M.; Tellez-Arredondo, P. Ind. Eng. Chem. Res. 2008, 47, 5723-5733.
14. Huang S. H.; Radosz M. Ind. Eng. Chem. Res. 1990, 29, 2284-2294.
15. Kontogeorgis G. M.; Voutsas, E. C.; Yakoumis, I. V.; Tassios, D. P. Ind. Eng. Chem. Res. 1996, 35, 4310-4318.
16. Holldorff, H.; Knapp, H. Fluid Phase Equilib. 1988, 44, 195-209.
17. Niini, A. Suom. Kemistil. A. 1938, 11, 19-20.
18. Sadovnikova, L. V.; Komarova, V. F.; Aleksandrova, M. V.; Serafimov, L. A. Izv. Vyssh. Uchebn. Zaved., Khim. Khim. Tekhnol. 1972, 15, 1891-1894.
19. Huemer, H.; Wortl, K.; Moser, F. Fluid Phase Equilib. 1983, 11, 311-323.
20. Naradoslawsky, M.; Huemer, H.; Moser, F. Monatsh. Chem. 1987, 118, 1129-1142.
21. Ruiz, F.; Gomis, V.; Botella, R. F. Ind. Eng. Chem., 1988, 27, 648-650.
22. Liu, D.; Li, Q.; Chen, Z. Tianranqi Huagong 1994, 19, 52-58.
23. Malagoni, R. A.; Franco Jr., M. R. Fluid Phase Equilib. 2007, 255, 93-97.
24. Van Arkel, A. E.; Vles, S. E. Recl. Trav. Chim. Pays-Bas 1936, 55, 407-411.
25. Staverman, A. J. Recl. Trav. Chim. Pays-Bas 1941, 60, 836-841.
26. McGovern, E. W. Ind. Eng. Chem. 1943, 35, 1230-1239.
27. Stephenson, R. M. J. Chem. Eng. Data. 1992, 37, 80-95.
28. Krupatkin, I. L.; Glagoleva, M. F. Zh. Prikl. Khim. 1969, 42, 1526-1531.
29. Pearson, C. R.; McConnell, G. Proc. R. Soc. Lond. B. 1975, 189, 305-332.
30. Coca, J.; Diaz, R. M.; Pazos, C. Fluid Phase Equilib. 1980, 4, 125-136.
31. Gibby, C. W.; Hall, J. J. Chem. Soc. 1931, 691-693
32. Gross, P. M.; Saylor, J. H. J. Am. Chem. Soc. 1931, 53, 1744-1751.
33. Matin, N. B.; Zilberman, E. N.; Trachenko, V. I.; Afanasev, V. A. Zh. Prikl. Khim. 1980, 53, 1880-1882.
34. Bevia, F. R.; Rico, D. P. Fluid Phase Equilib. 1983, 10, 77-93.
35. Lo, J. M.; Tseng, C.-L.; Yang, J. Y. Anal. Chem. 1986, 58, 1596-1597.
36. Clifford, C. W. J. Ind. Eng. Chem., 1921, 13, 631-632.
37. Gross, P. M. J. Am. Chem. Soc. 1929, 51, 2362-2366.
38. Donahue, D. J.; Bartell, F. E. J. Phys. Chem., 1952, 56, 480-484.
39. Abramov, A. A. Zh. Fiz. Khim., 1995, 69, 1722-1723.
40. Horvath, A. L.; Getzen, F. W.; Maczynska, Z. J. Phys. Chem. Ref. Data. 1999, 28, 395-627.
41. Horvath, A. L.; Getzen, F. W. J. Phys. Chem. Ref. Data. 1999, 28, 649-777.
42. Mączyński, A.; Wisniewska-Gocłowska, B.; Goral, M. J. Phys. Chem. Ref. Data. 2004, 33, 549-577.
Glossary
a: mixture dispersive parameter
a
ij
: dispersive parameter for the pair i-j
b: co-volume
E
ij
: energy of association
f
ij
: Meyer function
F
ob
: objective function
k
ij
: binary interaction parameter
p, p
c
: pressure, critical pressure
R: gas constant
T, T
c
, T
r
: temperature, critical temperature, reduced temperature
v: molar volume
v
ij
: characteristic volume of association
x
i
, y
i
, w
i
: mole fractions of component i
z: compressibility
α: correction function parameter
δ
ij
: correction function parameter
φ
i
: correction function
φ
I
: fugacity coefficient of component i
η
I
: correction function parameter
τ
I
: correction function parameter
ω: vector of adjustable parameters
ω
i
: Pitzer’s acentric factor
AAD : average absolute deviation
CHC : chlorohydrocarbon
CPA : cubic plus association
CSDRK: Carnahan-Starling-De Santis-Redlich-Kwong
CTS : Cubic Two State
EoS: equation of State
HC: hydrocarbon
LLE: liquid-liquid equilibrium
NRTL: non-random two liquid model
SAFT: statistical association fluid theory
SRK: Soave-Redlich-Kwong
VLE : vapor-liquid equilibrium
VLLE: vapor-liquid-liquid equilibrium
Author notes
*Corresponding author: Milton Medeiros, e-mail: milton.medeiros@unam.mx; Tel: (+5255) 5622-3899 Ext. 44463. Departamento de Fisicoquímica, Facultad de Química, Universidad Nacional Autónoma de México, Ciudad Universitaria, México DF 04510, México.

 cygnusmind
cygnusmind